题目内容
【题目】如图,已知△ABC,按如下步骤作图: ①分别以A,C为圆心,大于 ![]() AC的长为半径画弧,两弧交于P,Q两点;
AC的长为半径画弧,两弧交于P,Q两点;
②作直线PQ,分别交AB,AC于点E,D,连接CE;
③过C作CF∥AB交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
【答案】
(1)证明:由作图知:PQ为线段AC的垂直平分线,
∴AE=CE,AD=CD,
∵CF∥AB
∴∠EAC=∠FCA,∠CFD=∠AED,
在△AED与△CFD中,
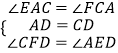 ,
,
∴△AED≌△CFD
(2)解:∵△AED≌△CFD,
∴AE=CF,
∵EF为线段AC的垂直平分线,
∴EC=EA,FC=FA,
∴EC=EA=FC=FA,
∴四边形AECF为菱形
【解析】(1)由作图知:PQ为线段AC的垂直平分线,从而得到AE=CE,AD=CD,然后根据CF∥AB得到∠EAC=∠FCA,∠CFD=∠AED,利用ASA证得两三角形全等即可;(2)根据全等得到AE=CF,然后根据EF为线段AC的垂直平分线,得到EC=EA,FC=FA,从而得到EC=EA=FC=FA,利用四边相等的四边形是菱形判定四边形AECF为菱形.
【考点精析】解答此题的关键在于理解菱形的判定方法的相关知识,掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目


