Question

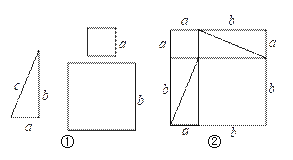
【题目】如图①是1个直角三角形和2个小正方形，直角三角形的三条边长分别是a、b、c，其中a、b是直角边．2个小正方形的边长分别是a、b．

（1）将4个完全一样的直角三角形和2个小正方形构成一个大正方形(如图②)．用两种不同的方法列代数式表示图②中的大正方形面积：方法一：_______；方法二：_____；

（2）观察图②，试写出(a+b)2，a2，2ab，b2这四个代数式之间的等量关系，为___ ____；

（3）利用你发现的结论，求：9922+16×992+64的值．

Answer 1

【答案】（1）方法一：(a+b)2；方法二：a2+2ab+b2；（2）(a+b)2=a2+2ab+b2；（3）1000000．

【解析】试题分析：（1）利用两种方法表示出大正方形面积即可；

（2）写出四个代数式之间的等量关系即可；

（3）利用得出的结果把原式变形，计算即可得到结果．

试题解析：（1）方法一：(a+b)2；方法二：a2+2ab+b2；

（2）(a+b)2=a2+2ab+b2；

（3）9922+16×992+64=9922+2×992×8+82=(992+8)2=10002=1000000．