题目内容
(1997•北京)已知:关于x的方程x2-3x+2k-1=0的两个实数根的平方和不小于这两个根的积,且反比例函数y=
的图象的两个分支在各自的象限内y随x的增大而减小.求满足上述条件的k的整数值.
| 1+2k | x |
分析:先根据根的判别式得到△=(-3)2-4(2k-1)≥0,解得k≤
;再根据根与系数的关系得x1+x2=3,x1•x2=2k-1,由x12+x22≥x1x2得到9-3(2k-1)≥0,解得k≤2,
然后利用反比例函数的性质得到1+2k>0,即k>-
,则k的取值范围为-
<k≤
,再找出此范围内的整数即可.
| 13 |
| 8 |
然后利用反比例函数的性质得到1+2k>0,即k>-
| 1 |
| 2 |
| 1 |
| 2 |
| 13 |
| 8 |
解答:解:∵关于x的方程x2-3x+2k-1=0有两个实数根,
∴△=(-3)2-4(2k-1)≥0,解得k≤
,
设方程x2-3x+2k-1=0的两个根为x1、x2,则x1+x2=3,x1•x2=2k-1,
∵x12+x22≥x1x2,即(x1+x2)2-3x1x2≥0,
∴9-3(2k-1)≥0,解得k≤2,
∴k≤
,
∵反比例函数y=
的图象的两个分支在各自的象限内y随x的增大而减小,
∴1+2k>0,即k>-
,
∴k的取值范围为-
<k≤
,
∴k的整数值为0、1.
∴△=(-3)2-4(2k-1)≥0,解得k≤
| 13 |
| 8 |
设方程x2-3x+2k-1=0的两个根为x1、x2,则x1+x2=3,x1•x2=2k-1,
∵x12+x22≥x1x2,即(x1+x2)2-3x1x2≥0,
∴9-3(2k-1)≥0,解得k≤2,
∴k≤
| 13 |
| 8 |
∵反比例函数y=
| 1+2k |
| x |
∴1+2k>0,即k>-
| 1 |
| 2 |
∴k的取值范围为-
| 1 |
| 2 |
| 13 |
| 8 |
∴k的整数值为0、1.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-
,x1•x2=
.也考查了一元二次方程根的判别式以及反比例函数的性质.
| b |
| a |
| c |
| a |

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
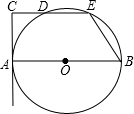 (1997•北京)已知,如图,AB为⊙O的直径,AC与⊙O相切于点A,CE∥AB交⊙O于D、E.求证:EB2=CD•AB.
(1997•北京)已知,如图,AB为⊙O的直径,AC与⊙O相切于点A,CE∥AB交⊙O于D、E.求证:EB2=CD•AB. ,并且OC>OE.
,并且OC>OE.