Question

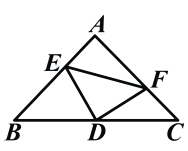
【题目】如图，在△ABC中，以BC为直径的圆交AC于点D，∠ABD＝∠ACB.

(1)求证：AB是圆的切线；

(2)若点E是BC上一点，已知BE＝4 ,tan∠AEB＝，AB∶BC＝2∶3，求圆的直径．

Answer 1

【答案】(1)详见解析；（2）10.

【解析】

试题分析：(1)根据∠ABD＝∠ACB和∠ACB＋∠DBC＝ 90°可得∠ABC＝90°，然后根据切线的判定定理可判断AB是圆的切线；(2) 根据BE＝4 ,tan∠AEB＝先求出AB的长，再根据AB∶BC＝2∶3求出BC的长，即得直径.

试题解析：(1)证明：∵BC是直径，∴∠BDC＝90°,∴∠ACB＋∠DBC＝ 90°.

又∵∠ABD＝∠ACB,∴∠ABD＋∠DBC＝90°,∴AB⊥BC.

又∵点B在圆上，∴AB是圆的切线．

(2)解：在Rt△AEB中，tan∠AEB＝，∴＝，即AB＝BE＝×4＝．

∵AB∶BC＝2∶3，∴BC＝AB＝×＝10.

∴圆的直径为10.