题目内容
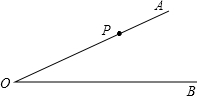 已知∠AOB=30°,P是OA上的一点,OP=24cm,以r为半径作⊙P.
已知∠AOB=30°,P是OA上的一点,OP=24cm,以r为半径作⊙P.
(1)若r=12cm,试判断⊙P与OB位置关系;
(2)若⊙P与OB相离,试求出r需满足的条件.
解:过点P作PC⊥OB,垂足为C,则∠OCP=90°.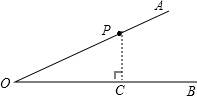
∵∠AOB=30°,OP=24cm,
∴PC= OP=12cm.
OP=12cm.
(1)当r=12cm时,r=PC,
∴⊙P与OB相切,
即⊙P与OB位置关系是相切.
(2)当⊙P与OB相离时,r<PC,
∴r需满足的条件是:0cm<r<12cm.
分析:(1)过点P作PC⊥OB,垂足为C根据含30度角的直角三角形性质求出PC,得出PC=r,则得出⊙P与OB位置关系是相切;
(2)根据相切时半径=12,再根据当r<d时相离,即可求出答案.
点评:本题考查了直线与圆的位置关系和含30度角的直角三角形性质,注意:已知圆的半径r,圆心到直线l的距离为d,①当d>r时,直线l与圆相离,②当d=r时,直线l与圆相切,③当d<r时,直线l与圆相交.

∵∠AOB=30°,OP=24cm,
∴PC=
 OP=12cm.
OP=12cm.(1)当r=12cm时,r=PC,
∴⊙P与OB相切,
即⊙P与OB位置关系是相切.
(2)当⊙P与OB相离时,r<PC,
∴r需满足的条件是:0cm<r<12cm.
分析:(1)过点P作PC⊥OB,垂足为C根据含30度角的直角三角形性质求出PC,得出PC=r,则得出⊙P与OB位置关系是相切;
(2)根据相切时半径=12,再根据当r<d时相离,即可求出答案.
点评:本题考查了直线与圆的位置关系和含30度角的直角三角形性质,注意:已知圆的半径r,圆心到直线l的距离为d,①当d>r时,直线l与圆相离,②当d=r时,直线l与圆相切,③当d<r时,直线l与圆相交.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
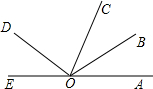 如图,E,O,A三点共线,OB平分∠AOC,∠DOC=2∠EOD,已知∠AOB=30°,则∠EOD的度数为
如图,E,O,A三点共线,OB平分∠AOC,∠DOC=2∠EOD,已知∠AOB=30°,则∠EOD的度数为