题目内容
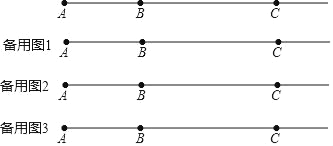
【题目】如图，直线l上依次有三点A、B、C，且AB=8、BC=16，点P为射线AB上一动点，将线段AP进行翻折得到线段PA′（点A落在直线l上点A′处、线段AP上的所有点与线段PA′上的点对应）．
（1）若翻折后A′C=2，则翻折前线段AP= ．
（2）若点P在线段BC上运动，点M为线段A′C的中点，直接写出线段PM的长度．
【答案】（1）11或13；（2）12．
【解析】
（1）分两种情况讨论：①A′落在C的左侧；②A′落在C的右侧；
（2）分①当A′在线段BC上，②当A′在l上且在C的右侧，进行讨论即可求解．
（1）①当A′落在C的左侧时，AC=AB+BC=8+16=24，AA′=AC﹣A′C=24﹣2=22．
AP=22÷2=11；
②当A′落在C的右侧时，AC=AB+BC=8+16=24，AA′=AC+A′C=24+2=26．
AP=26÷2=13．
故答案为：11或13；
（2）①如备用图1，当A′在线段BC上，由题知PA=PA′．
∵M为A′C中点，∴MA′=MC，∴PM=PA′+A′M=
AA′+AC=×AC=×24=12；
②如备用图2，当A′在直线l上且在C的右侧．
∵M为A′C中点，∴MA′=MC，∴PM=PA′﹣A′M=AA′﹣A′C=AC=×24=12．
综上所述：PM=12．
练习册系列答案
相关题目
