题目内容
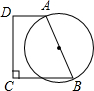如图，在直角梯形ABCD中，AD∥BC，∠D=90°，以斜边AB为直径作圆，已知AB=10，AD=m，BC=m+4，要使圆与折线BCDA有三个公共点（A、B两点除外），则m的取值范围是0＜m＜3
0＜m＜3
．分析：此题首先能够根据公共点的个数得到直线CD和圆的位置关系；再进一步计算出相切时，圆心到直线的距离，从而根据直线和圆的位置关系与数量之间的联系，得到答案．
若d＜r，则直线与圆相交；若d=r，则直线于圆相切；若d＞r，则直线与圆相离．
若d＜r，则直线与圆相交；若d=r，则直线于圆相切；若d＞r，则直线与圆相离．
解答：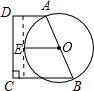
解：根据题意，得圆必须和直线CD相交．
设直线CD和圆相切于点E，连接OE，则OE⊥CD，
则OE∥AD∥BC，
又OA=OB，则ED=EC．
根据梯形的中位线定理，得OE=
=m+2，
则m+2=5，m=3，
所以直线要和圆相交，则0＜m＜3．
故答案为：0＜m＜3．
解：根据题意，得圆必须和直线CD相交．设直线CD和圆相切于点E，连接OE，则OE⊥CD，
则OE∥AD∥BC，
又OA=OB，则ED=EC．
根据梯形的中位线定理，得OE=
| m+m+4 |
| 2 |
则m+2=5，m=3，
所以直线要和圆相交，则0＜m＜3．
故答案为：0＜m＜3．
点评：考查了直线和圆的位置关系与数量之间的联系．这里要求m的取值范围，应求得相切时m的值，再进一步确定m的取值范围．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
20、如图，在直角梯形ABCD中，AD∥BC，CD⊥BC，E为BC边上的点．将直角梯形ABCD沿对角线BD折叠，使△ABD与△EBD重合（如图中阴影所示）．若∠A=130°，AB=4cm，则梯形ABCD的高CD≈
如图，在直角梯形ABCD中，AB∥DC，∠D=90°，AC⊥BC，AB=10cm，BC=6cm，F点以2cm/秒的速度在线段AB上由A向B匀速运动，E点同时以1cm/秒的速度在线段BC上由B向C匀速运动，设运动时间为t秒（0＜t＜5）．
（1998•大连）如图，在直角梯形ABCD中．AD∥BC，DC⊥BC，且BC=3AD．以梯形的高AE为直径的⊙O交AB于点F，交CD于点G、H．过点F引⊙O的切线交BC于点N．
BC上的动点，点G在AB上，且四边形AEFG是矩形．设FG=x，矩形AEFG的面积为y．