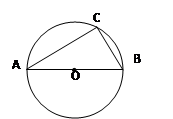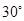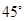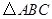题目内容
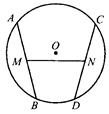
(1)如图1,已知△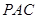 圆
圆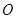 的内接正三角形,那么∠
的内接正三角形,那么∠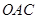 ﹦ ;
﹦ ;
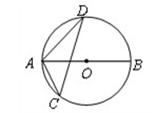
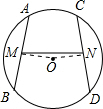
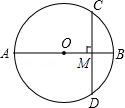
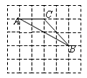
(2)如图2,设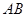 是圆
是圆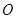 的直径,
的直径,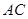 是圆的任意一条弦,∠
是圆的任意一条弦,∠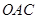 ﹦
﹦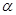 ﹒
﹒
① 如果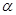 ﹦45°,那么
﹦45°,那么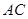 能否成为圆内接正多边形的一条边?若有可能,那么此多边形是几边形?请说明理由﹒
能否成为圆内接正多边形的一条边?若有可能,那么此多边形是几边形?请说明理由﹒
② 若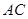 是圆的内接正
是圆的内接正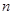 边形的一边,则用含
边形的一边,则用含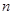 的代数式表示
的代数式表示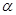 应为 ﹒
应为 ﹒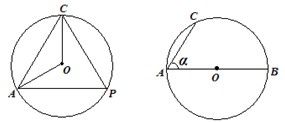
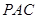 圆
圆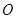 的内接正三角形,那么∠
的内接正三角形,那么∠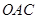 ﹦ ;
﹦ ;(2)如图2,设
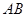 是圆
是圆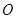 的直径,
的直径,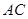 是圆的任意一条弦,∠
是圆的任意一条弦,∠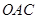 ﹦
﹦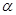 ﹒
﹒① 如果
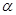 ﹦45°,那么
﹦45°,那么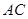 能否成为圆内接正多边形的一条边?若有可能,那么此多边形是几边形?请说明理由﹒
能否成为圆内接正多边形的一条边?若有可能,那么此多边形是几边形?请说明理由﹒② 若
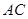 是圆的内接正
是圆的内接正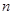 边形的一边,则用含
边形的一边,则用含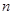 的代数式表示
的代数式表示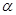 应为 ﹒
应为 ﹒
解:(1) 30°
(2) ①能﹒
∵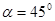 ,∴圆内接正多边形的一个内角为90°,∴是正方形﹒
,∴圆内接正多边形的一个内角为90°,∴是正方形﹒
②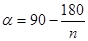
(2) ①能﹒
∵
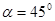 ,∴圆内接正多边形的一个内角为90°,∴是正方形﹒
,∴圆内接正多边形的一个内角为90°,∴是正方形﹒ ②
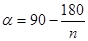
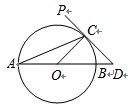
(1)先根据圆周角定理求出∠AOC的度数,再根据三角形内角和定理及等腰三角形的性质即可解答;
(2)①假设AC是圆内接多边形的一条边,则此多边形的内角为45°×2=90°,故此多边形是正方形;
②根据正多边形内角和定理即可求出答案.
(2)①假设AC是圆内接多边形的一条边,则此多边形的内角为45°×2=90°,故此多边形是正方形;
②根据正多边形内角和定理即可求出答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目