��Ŀ����
����Ŀ����ͼ����֪��AOB��60�����ڡ�AOB��ƽ����OM����һ��C����DCE��120��������DCE�Ķ������C�غϣ����������߷ֱ���ֱ��OA��OB�ཻ�ڵ�D��E��
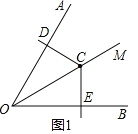
��1������DCE�Ƶ�C��ת��CD��OA��ֱʱ����ͼ1���������OE+OD��OC��������ϵ����˵�����ɣ�
��2���ɣ�ͼ1����λ�ý���DCE�Ƶ�C��ʱ����ת���ǣ�0������90�������߶�OD��OE��OC֮������������������ϵ����д����IJ��룬��˵�����ɣ�
���𰸡���1��OE+OD��![]() OC������������2��OD+OE��
OC������������2��OD+OE��![]() OC��OE��OD��
OC��OE��OD��![]() OC��������
OC��������
��������
��1�����жϳ���OCE��60��������������ǵ����Ǻ����ó�OD��OE��![]() OC�����ɵó����ۣ�
OC�����ɵó����ۣ�
��2�������������ͼ��ͬ��1���ķ�����OF+OG��![]() OC�����жϳ���CFD�ա�CGE���ó�DF��EG���������������ɵó����ۣ�
OC�����жϳ���CFD�ա�CGE���ó�DF��EG���������������ɵó����ۣ�
�⣺��1��OE+OD��![]() OC���������£�
OC���������£�
��OM�ǡ�AOB��ƽ���ߣ�
���AOC����BOC��![]() ��AOB��30����
��AOB��30����
��CD��OA�����ODC��90��
���OCD��60��
���OCE����DCE����OCD��60����
��Rt��OCD��OD��OCcos30����![]() OC��
OC��
ͬ����OE��![]() OC��
OC��
��OD+OE��![]() OC��
OC��
��2��OD+OE��![]() OC��OE��OD��
OC��OE��OD��![]() OC���������£�
OC���������£�
���籸��ͼ1������C��CF��OA�ڵ�F��CG��OB�ڵ�G��
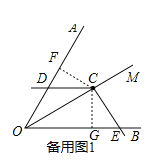
���OFC����OGC��90��
�ߡ�AOB��60����
���FCG��120����
ͬ��1���ķ����ã�OF��![]() OC��OG��
OC��OG��![]() OC��
OC��
��OF+OG��![]() OC��
OC��
��CF��OA��CG��OB���ҵ�C�ڡ�AOB��ƽ�����ϣ�
��CF��CG��
�ߡ�DCE����FCG��120����
���DCF����ECG��
���CFD�ա�CGE��ASA��
��DF��EG��
��OF��OD+DF��span>OD+EG��OG��OE��GE��
��OF+OG��OD+OE��
��OD+OE��![]() OC��
OC��
���籸��ͼ2������C��CF��OA�ڵ�F��CG��OB�ڵ�G��
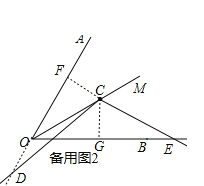
���OFC����OGC��90��
�ߡ�AOB��60����
���FCG��120����
ͬ��1���ķ����ã�OF��![]() OC��OG��
OC��OG��![]() OC��
OC��
��OF+OG��![]() OC��
OC��
��CF��OA��CG��OB���ҵ�C�ڡ�AOB��ƽ�����ϣ�
��CF��CG��
�ߡ�DCE����FCG��120����
���DCF����ECG��
���CFD�ա�CGE��ASA��
��DF��EG��
��OF��DF��OD��EG��OD��OG��OE��GE��
��OF+OG��OE��OD��
��OE��OD��![]() OC��
OC��
�����������߶�OD��OE��OC֮���������ϵΪ��OD+OE��![]() OC��OE��OD��
OC��OE��OD��![]() OC��
OC��

 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�