题目内容
【题目】定义:把一个半圆与抛物线的一部分组成的封闭图形称为“蛋圆”.
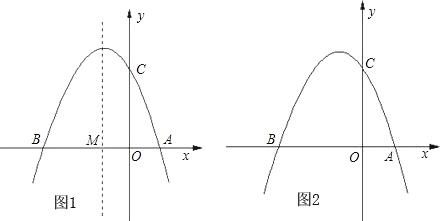
如图,抛物线y=x2﹣2x﹣3与x轴交于点A,B,与y轴交于点D,以AB为直径,在x轴上方作半圆交y轴于点C,半圆的圆心记为M,此时这个半圆与这条抛物线x轴下方部分组成的图形就称为“蛋圆”.
(1)直接写出点A,B,C的坐标及“蛋圆”弦CD的长;
A ,B ,C ,CD= ;
(2)如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.
①求经过点C的“蛋圆”切线的解析式;
②求经过点D的“蛋圆”切线的解析式;
(3)由(2)求得过点D的“蛋圆”切线与x轴交点记为E,点F是“蛋圆”上一动点,试问是否存在S△CDE=S△CDF,若存在请求出点F的坐标;若不存在,请说明理由;
(4)点P是“蛋圆”外一点,且满足∠BPC=60°,当BP最大时,请直接写出点P的坐标.
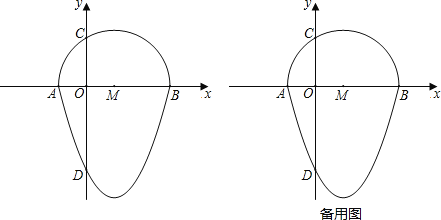
【答案】(1)A(﹣1,0),B(3,0),C(0,![]() ),CD=3+
),CD=3+![]() ;(2)①
;(2)①![]() ;②y=﹣2x﹣3;(3)F′(
;②y=﹣2x﹣3;(3)F′(![]() ,
,![]() ),F′′(
),F′′(![]() ,
,![]() );(4)点P的坐标为(1,2
);(4)点P的坐标为(1,2![]() ).
).
【解析】
(1)根据抛物线与一元二次方程的关系以及勾股定理解答;
(2)运用待定系数法求出经过点C的“蛋圆”切线的解析式;运用二元二次方程组、一元二次方程根的判别式求出过点D的“蛋圆”切线的解析式;
(3)根据题意求出点E的坐标,根据同底等高的两个三角形面积相等解答;
(4)根据∠BPC=60°保持不变,点P在一圆弧上运动和直径是最大的弦进行解答即可.
(1)当y=0时,x2﹣2x﹣3=0,
解得x1=﹣1,x2=3,
当x=0时,y=3,
∴A(﹣1,0),B(3,0),OD=3,
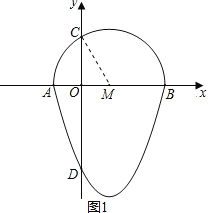
如图1,连接MC,由题意得,OM=1,MC=2,
∴OC=![]() ,
,
∴C(0,![]() ),CD=3+
),CD=3+![]() ,
,
故答案为:(﹣1,0);(3,0);(0,![]() );3+
);3+![]() ;
;
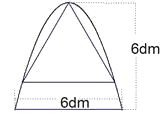
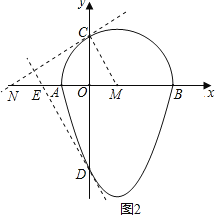
(2)①如图2,NC⊥CM,
∵∠CMO=∠NMC,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴N的坐标为(﹣3,0),
设NC的解析式为![]() ,
,
∴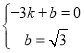 ,
,
∴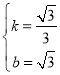 ,
,
∴经过点C的“蛋圆”切线的解析式为:![]() ,
,
②过点D的“蛋圆”切线的解析式为:y=kx﹣3,
由![]() ,
,
得:x2﹣(2+k)x=0,即:![]() ,
,
∵直线与抛物线只有一个交点,
∴![]() ,即k=﹣2,
,即k=﹣2,
∴经过点D的“蛋圆”切线的解析式为:y=﹣2x﹣3.
(3)如图3,∵经过点D的“蛋圆”切线的解析式为:y=﹣2x﹣3,
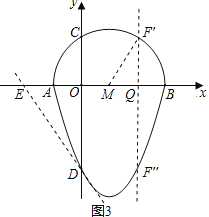
∴E点坐标为(![]() ,0),
,0),
∵S△CDE=S△CDF,
∴F点的横坐标为![]() ,
,
在Rt△MQF1中
![]() ,
,![]() ,
,
∴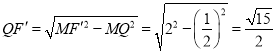 ,
,

把x=![]() 代入y=x2﹣2x﹣3,可求得y=
代入y=x2﹣2x﹣3,可求得y=![]() .
.
∴F′(![]() ,
,![]() ),F′′(
),F′′(![]() ,
,![]() );
);
(4)如图4,∵∠BPC=60°保持不变,
因此点P在一圆弧上运动.
此圆是以K为圆心(K在BC的垂直平分线上,且∠BKC=120°),BK为半径.
当BP为直径时,BP最大.
∵B(3,0),C(0,![]() ),
),
∴OB=![]() ,OC
,OC![]() ,
,
∴![]() ,
,
∵BP为直径,
∴∠PCB=90°,
∵∠BPC=60°
∴![]() ,
,![]() ,即:
,即:![]() ,
,
∴![]() ,
,
过点P作PR⊥y轴于点R,
∵∠RCP+∠PCB+∠OCB=180![]() ,
,
∴∠RCP+∠OCB=90![]() ,
,
∠OBC+∠OCB=90![]() ,
,
∴∠RCP=∠OBC,
∴![]()
∴![]()
∴![]()
∴PR=1,RC=![]() .
.
所以点P的坐标为(1,2![]() ).
).
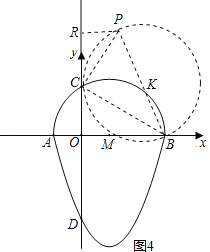

 阅读快车系列答案
阅读快车系列答案【题目】某工厂设计了一款成本为20元件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价x(元件) | … | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(1)研究发现,每天销售量y与单价x满足一次函数关系,求出y与x的关系式;
(2)当地物价部门规定,该工艺品销售单价最高不能超过50元件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?