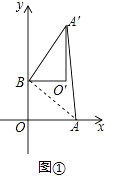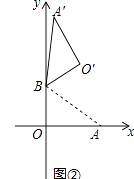ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΫΪ“ΜΗ±»ΐΫ«Αε÷–ΒΡΝΫΩι÷±Ϋ«»ΐΫ«≥ΏΒΡ÷±Ϋ«ΕΞΒψOΑ¥»γΆΦΖΫ ΫΒΰΖ≈‘Ύ“ΜΤπΘ°
Θ®1Θ©»γΆΦΘ®1Θ©»τΓœBOD=35ΓψΘ§«σΓœAOCΒΡΕ» ΐΘ§»τΓœAOC=135ΓψΘ§«σΓœBODΒΡΕ» ΐΓΘ
Θ®2Θ©»γΆΦΘ®2Θ©»τΓœAOC=150ΓψΘ§«σΓœBODΒΡΕ» ΐ
Θ®3Θ©≤¬œκΓœAOC”κΓœBODΒΡ ΐΝΩΙΊœΒΘ§≤ΔΫαΚœΆΦΘ®1Θ©ΥΒΟςάμ”…Θ°
Θ®4Θ©»ΐΫ«≥ΏAOB≤ΜΕ·Θ§ΫΪ»ΐΫ«≥ΏCODΒΡOD±Ώ”κOA±Ώ÷ΊΚœΘ§»ΜΚσ»ΤΒψOΑ¥Υ≥ ±’κΜρΡφ ±’κΖΫœρ»Έ“βΉΣΕ·“ΜΗωΫ«Ε»Θ§Β±ΓœAODΘ®0ΓψΘΦΓœAODΘΦ90ΓψΘ©Β»”ΎΕύ…ΌΕ» ±Θ§’βΝΫΩι»ΐΫ«≥ΏΗς”–“ΜΧθ±ΏΜΞœύ¥Ι÷±Θ§÷±Ϋ”–¥≥ωΓœAODΫ«Ε»Υυ”–Ω…ΡήΒΡ÷ΒΘ§≤Μ”ΟΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©45ΓψΘΜΘ®2Θ©30ΓψΘΜΘ®2Θ©ΓœACB”κΓœDCEΜΞ≤ΙΘΜΘ®4Θ©30Γψ.45Γψ.60Γψ.75Γψ
ΓΨΫβΈωΓΩ
’ϊΧε
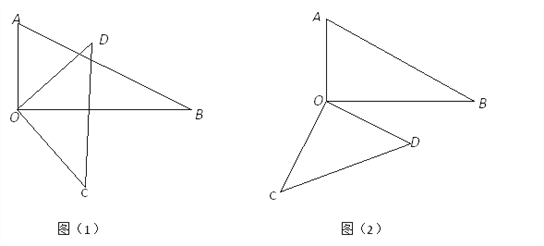
(1)ΗυΨίΓœAOCΘ§ΓœAOBΘ§ΓœCODΘ§ΓœBODΒΡΚΆ≤νΙΊœΒ«σΫβΘΜ(2)”Ο÷ήΫ«Φθ»Ξ“―÷ΣΫ«ΒΡΕ» ΐΘΜ(3)ΗυΨί(1)ΚΆ(2)÷–ΒΡΫαΙϊ≤¬œκΘΜ(4)ΝΫΩι»ΐΫ«≥ΏΗς”–“ΜΧθ±ΏΜΞœύ¥Ι÷±”–ΥΡ÷÷–Έ ΫΘ§–η“ΣΖ÷άύΧ÷¬έ.
ΫβΘΚ(1)»τΓœBOD=35ΓψΘ§ΓΏΓœAOB=ΓœCOD=90ΓψΘ§
ΓύΓœAOC=ΓœAOB+ΓœCOD©¹ΓœBOD=90Γψ+90Γψ©¹35Γψ=145ΓψΘ§
»τΓœAOC=135ΓψΘ§
‘ρΓœBOD=ΓœAOB+ΓœCOD©¹ΓœAOC=90Γψ+90Γψ©¹135Γψ=45ΓψΘΜ
(2)»γΆΦ2Θ§»τΓœAOC=150ΓψΘ§
‘ρΓœBOD=360Γψ©¹ΓœAOC©¹ΓœAOB©¹ΓœCOD=30ΓψΘΜ
(3)ΓœAOC”κΓœBODΜΞ≤ΙΘ°
ΓΏΓœAOD+ΓœBOD+ΓœBOD+ΓœBOC=180ΓψΘ°
ΓΏΓœAOD+ΓœBOD+ΓœBOC=ΓœAOCΘ§
ΓύΓœAOC+ΓœBOD=180ΓψΘ§Φ¥ΓœACB”κΓœDCEΜΞ≤ΙΘ°
(4)ODΓΆAB ±Θ§ΓœAOD=30ΓψΘ§
CDΓΆOB ±Θ§ΓœAOD=45ΓψΘ§
CDΓΆAB ±Θ§ΓœAOD=75ΓψΘ§
OCΓΆAB ±Θ§ΓœAOD=60ΓψΘ§
Φ¥ΓœAODΫ«Ε»Υυ”–Ω…ΡήΒΡ÷ΒΈΣΘΚ30ΓψΘΜ45ΓψΘΜ60ΓψΘΜ75Γψ.

 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ