题目内容
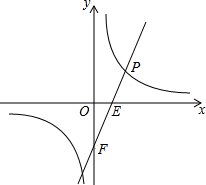 已知一次函数y=kx+b的图象与反比例函数
已知一次函数y=kx+b的图象与反比例函数 的图象交于点P(2,1),与x轴交于点E,与y轴交于点F,O是坐标原点.
的图象交于点P(2,1),与x轴交于点E,与y轴交于点F,O是坐标原点.
(1)求这两个函数的解析式;
(2)能否在反比例函数 的图象上找到一点H,使△HOE的面积与△EOF的面积
的图象上找到一点H,使△HOE的面积与△EOF的面积
相等?如果能,请求出点H的坐标;如果不能,请说明理由.
解:(1)把P(2,1)代入y= 得:k=2,
得:k=2,
故反比例函数的解析式是y= ,
,
把点P(2,1),k=2代入一次函数y=kx+b得,2×2+b=1,
解得b=-3.
所以,一次函数的解析式为y=2x-3;
(2)令y=0,则2x-3=0,解得x= ,
,
令x=0,则y=-3,
所以,点E( ,0),F(0,-3),
,0),F(0,-3),
∴OE= ,OF=3,
,OF=3,
设点H到x轴的距离为h,
则S△HOE= ×
× h=
h= h,S△EOF=
h,S△EOF= ×
× ×3=
×3= ,
,
所以, h=
h= ,
,
解得h=3,
即点H的纵坐标的绝对值是3,
当H的纵坐标是负数时, =-3,解得x=-
=-3,解得x=- ,
,
当点H的纵坐标是正数时, =3,解得x=
=3,解得x= ,
,
所以,点H的坐标为(- ,-3)或(
,-3)或( ,3).
,3).
分析:(1)把点P的坐标代入反比例函数解析式求出k的值,再把k的值与点P的坐标代入一次函数解析式计算求出b的值,即可得解;
(2)利用直线解析式求出E、F的坐标,从而得到OE、OF的长度,然后根据三角形的面积求出点H到x轴的距离,再分点H纵坐标为负数与正数两种情况解答.
点评:本题考查了反比例函数与一次函数的交点问题,主要利用了待定系数法求反比例函数解析式,求一次函数解析式,(1)一次函数与反比例函数的比例系数都是k是解题的关键,(2)要注意分点H的纵坐标是负数与正数两种情况讨论.
 得:k=2,
得:k=2,故反比例函数的解析式是y=
 ,
,把点P(2,1),k=2代入一次函数y=kx+b得,2×2+b=1,
解得b=-3.
所以,一次函数的解析式为y=2x-3;
(2)令y=0,则2x-3=0,解得x=
 ,
,令x=0,则y=-3,
所以,点E(
 ,0),F(0,-3),
,0),F(0,-3),∴OE=
 ,OF=3,
,OF=3,设点H到x轴的距离为h,
则S△HOE=
 ×
× h=
h= h,S△EOF=
h,S△EOF= ×
× ×3=
×3= ,
,所以,
 h=
h= ,
,解得h=3,
即点H的纵坐标的绝对值是3,
当H的纵坐标是负数时,
 =-3,解得x=-
=-3,解得x=- ,
,当点H的纵坐标是正数时,
 =3,解得x=
=3,解得x= ,
,所以,点H的坐标为(-
 ,-3)或(
,-3)或( ,3).
,3).分析:(1)把点P的坐标代入反比例函数解析式求出k的值,再把k的值与点P的坐标代入一次函数解析式计算求出b的值,即可得解;
(2)利用直线解析式求出E、F的坐标,从而得到OE、OF的长度,然后根据三角形的面积求出点H到x轴的距离,再分点H纵坐标为负数与正数两种情况解答.
点评:本题考查了反比例函数与一次函数的交点问题,主要利用了待定系数法求反比例函数解析式,求一次函数解析式,(1)一次函数与反比例函数的比例系数都是k是解题的关键,(2)要注意分点H的纵坐标是负数与正数两种情况讨论.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
 已知一次函数y=kx+2的图象经过A(-1,1).
已知一次函数y=kx+2的图象经过A(-1,1). m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.
m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.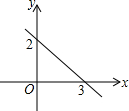 已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.
已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.