ЬтФПФкШн
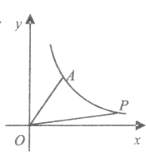
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌЕуAЁЂBЁЂCдкxжсЩЯЃЌЕуDЁЂEдкyжсЩЯЃЌOA=OD=2ЃЌOC=OE=4ЃЌBЮЊЯпЖЮOAЕФжаЕуЃЌжБЯпADгыОЙ§BЁЂEЁЂCШ§ЕуЕФХзЮяЯпНЛгкFЁЂGСНЕуЃЌгыЦфЖдГЦжсНЛгкMЃЎ
ЃЈ1ЃЉЧѓОЙ§BЁЂEЁЂCШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуPЮЊЯпЖЮFGЩЯвЛИіЖЏЕуЃЈгыFЁЂGВЛжиКЯЃЉЃЌЕБPдкЪВУДЮЛжУЪБЃЌвдPЁЂOЁЂCЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЌЧыЧѓГіДЫЪБЕуPЕФзјБъЃЛ
ЃЈ3ЃЉШєЕуPЮЊжБЯпFGЩЯвЛИіЖЏЕуЃЌQЮЊХзЮяЯпЩЯШЮвЛЕуЃЌХзЮяЯпЕФЖЅЕуЮЊNЃЌЬНОПвдPЁЂQЁЂMЁЂNЮЊЖЅЕуЕФЫФБпаЮФмЗёГЩЮЊЦНааЫФБпаЮЃПШєФмЃЌЧыжБНгаДГіЕуPЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
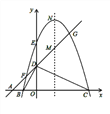
ЁОД№АИЁП(1) y=Љx2+3x+4ЃЛ(2) PзјБъЪЧЃЈ2ЃЌ4ЃЉЃЛ(3)МћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓЕУЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉИљОнЕШбќШ§НЧаЮЕФЖЈвхЃЌЗжOP=OCЃЌPC=OCЃЌOP=PCШ§жжЧщПіМДПЩЧѓЕУPЕФзјБъЃЛ
ЃЈ3ЃЉЩшЕуPЮЊЃЈxЃЌx+2ЃЉQЃЈxЃЌ-x2+3x+4ЃЉЃЌдђPQ=-x2+2x+2ЃЌИљОнPQNMЪЧЦНааЫФБпаЮЃЌдђPQ=MNЃЌМДПЩЧѓЕУPMЕФГЄЃЌХаЖЯЪЧЗёГЩСЂЃЌДгЖјШЗЖЈPЕФзјБъЃЎ
ЃЈ1ЃЉЁпBЃЈ-1ЃЌ0ЃЉEЃЈ0ЃЌ4ЃЉCЃЈ4ЃЌ0ЃЉ
ЩшНтЮіЪНЪЧy=ax2+bx+c
ПЩЕУ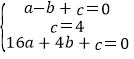 ЃЌНтЕУ
ЃЌНтЕУ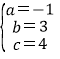
Ёрy=-x2+3x+4ЃЛ
ЃЈ2ЃЉЁпЕуAзјБъЪЧЃЈ-2ЃЌ0ЃЉЃЌЕуDзјБъЪЧЃЈ0ЃЌ2ЃЉ
жБЯпADЕФНтЮіЪНЪЧy=x+2ЃЌ
ЩшЕуPзјБъЪЧЃЈxЃЌx+2ЃЉЃЌ
ЕБOP=OCЪБЃЌx2+ЃЈx+2ЃЉ2=16НтЕУxЃН1ЁР![]() ЃЈxЃН1
ЃЈxЃН1![]() ВЛЗћКЯЃЌЩсШЅЃЉДЫЪБЕуPЃЈ1+
ВЛЗћКЯЃЌЩсШЅЃЉДЫЪБЕуPЃЈ1+![]() ЃЌ3+
ЃЌ3+![]() ЃЉЃЌ
ЃЉЃЌ
ЕБPC=OCЪБЃЌЃЈx+2ЃЉ2+ЃЈ4-xЃЉ2=16ЗНГЬЮоНтЃЌ
ЕБPO=PCЪБЃЌЕуPдкOCЕФжаДЙЯпЩЯЃЌ
ЁрЕуPКсзјБъЪЧ2ЃЌЕУЕуPзјБъЪЧЃЈ2ЃЌ4ЃЉЃЌ
ЁрЕБЁїPOCЪЧЕШбќШ§НЧаЮЪБЃЌЕуPзјБъЪЧЃЈ1+![]() ЃЌ3+
ЃЌ3+![]() ЃЉЛђЃЈ2ЃЌ4ЃЉЃЛ
ЃЉЛђЃЈ2ЃЌ4ЃЉЃЛ
ЃЈ3ЃЉ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()

 НзЬнМЦЫуЯЕСаД№АИ
НзЬнМЦЫуЯЕСаД№АИ