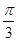题目内容
如图,直线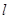 的解析式为
的解析式为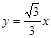 ,⊙
,⊙ 是以坐标原点为圆心,半径为1的圆,点
是以坐标原点为圆心,半径为1的圆,点 在
在 轴上运动,过点
轴上运动,过点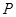 且与直线
且与直线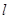 平行(或重合)的直线与⊙
平行(或重合)的直线与⊙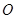 有公共点,则点
有公共点,则点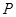 的横坐标为整数的点的个数有 ▲ 个.
的横坐标为整数的点的个数有 ▲ 个.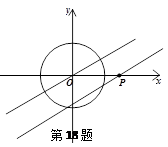
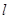 的解析式为
的解析式为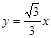 ,⊙
,⊙ 是以坐标原点为圆心,半径为1的圆,点
是以坐标原点为圆心,半径为1的圆,点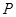 在
在 轴上运动,过点
轴上运动,过点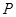 且与直线
且与直线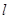 平行(或重合)的直线与⊙
平行(或重合)的直线与⊙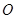 有公共点,则点
有公共点,则点 的横坐标为整数的点的个数有 ▲ 个.
的横坐标为整数的点的个数有 ▲ 个.
5
∵直线l的解析式为y= x,
x,
∴∠1=30°,
当过点P且与直线l平行的直线与圆O相切,且切点在第二象限时,如图所示,
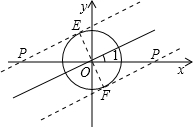
此时直线PE与圆O相切,切点为点E,
∵直线l∥PE,∠1=30°,
∴∠EPO=30°,
在Rt△PEO中,OE=1,
可得OP=2OE=2,又P在x轴负半轴上,
∴此时P坐标为(-2,0);
当过点P且与直线l平行的直线与圆O相切,且切点在第四象限时,如图所示,
此时直线PF与圆O相切,切点为点F,
∵直线l∥PF,∠1=30°,
∴∠FPO=30°,
在Rt△PFO中,OF=1,
可得OP=2OF=2,又P在x轴正半轴上,
∴此时P的坐标为(2,0),
综上,满足题意的点P横坐标p的范围是-2≤p≤2,
则点P的横坐标为整数的点的个数有-2,-1,0,1,2,共5个.
 x,
x,∴∠1=30°,
当过点P且与直线l平行的直线与圆O相切,且切点在第二象限时,如图所示,

此时直线PE与圆O相切,切点为点E,
∵直线l∥PE,∠1=30°,
∴∠EPO=30°,
在Rt△PEO中,OE=1,
可得OP=2OE=2,又P在x轴负半轴上,
∴此时P坐标为(-2,0);
当过点P且与直线l平行的直线与圆O相切,且切点在第四象限时,如图所示,
此时直线PF与圆O相切,切点为点F,
∵直线l∥PF,∠1=30°,
∴∠FPO=30°,
在Rt△PFO中,OF=1,
可得OP=2OF=2,又P在x轴正半轴上,
∴此时P的坐标为(2,0),
综上,满足题意的点P横坐标p的范围是-2≤p≤2,
则点P的横坐标为整数的点的个数有-2,-1,0,1,2,共5个.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
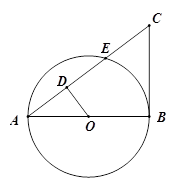
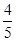 ,求OD的长.
,求OD的长. 所对圆周角∠ACB的度数是( )
所对圆周角∠ACB的度数是( )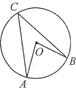
 ★”表示.并给出证明;我的命题是: .
★”表示.并给出证明;我的命题是: .
 是⊙O的直径,
是⊙O的直径, 是⊙O上的两点,若
是⊙O上的两点,若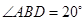 ,则
,则 的度数为( )
的度数为( )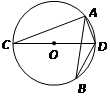

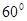
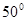
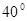
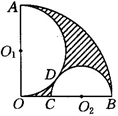
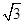 ,BC=1.则图中阴影部分所表示的扇形AOD的面积为( )
,BC=1.则图中阴影部分所表示的扇形AOD的面积为( )