Question

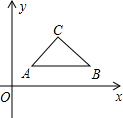（2013•杭州一模）如图，平面直角坐标系中，△ABC的顶点坐标分别是A（1，1），B（3，1），C（2，2），当直线y=

1

2

x+b与△ABC有交点时，b的取值范围是（　　）

• A．-1≤≤1
• B．-

  1

  2

  ≤b≤1
• C．-

  1

  2

  ≤b≤

  1

  2

• D．-1≤b≤

  1

  2

Answer 1

分析：将A（1，1），B（3，1），C（2，2）的坐标分别代入直线y=

1

2

x+b中求得b的值，再根据一次函数的增减性即可得到b的取值范围．

解答：解：将A（1，1）代入直线y=

1

2

x+b中，可得

1

2

+b=1，解得b=

1

2

；
将B（3，1）代入直线y=

1

2

x+b中，可得

3

2

+b=1，解得b=-

1

2

；
将C（2，2）代入直线y=

1

2

x+b中，可得1+b=2，解得b=1．
故b的取值范围是-

1

2

≤b≤1．
故选B．

点评：考查了一次函数的性质：k＞0，y随x的增大而增大，函数从左到右上升；k＜0，y随x的增大而减小，函数从左到右下降．