题目内容
两个全等的Rt△ABC和Rt△DEF重叠在一起,其中∠A=60°,∠ACB=∠DFE=90°且AC=1.固定△ABC不动,将△DEF作如下操作:
(1)如图1,△DEF沿线段AB向右平移(即D点在线段AB内移动),连接DC、CF、FB,四边形CDBF的面积会变吗?若不变请求出其面积;


(2)如图2,当D点移到AB中点时,连接DC、CF、FB,BC与DF相交于点O.除Rt△ABC≌Rt△DEF外,请找出图中其他所有全等三角形,不必写理由;
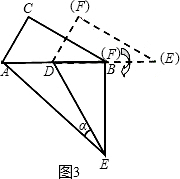
(3)如图3,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连接AE,求:sin∠α的值.
解:(1)因为S四边形CDBF=S三角形CDF+S三角形FDB=S三角形CAD+S三角形CDB=S△ABC,
所以四边形CDBF的面积不会变.
S四边形CDBF=S△ABC= ×2×
×2× =
= .
.
(2)△COD≌△BOD≌△BOF≌△COF;
△ACD≌△FCD≌△BFD;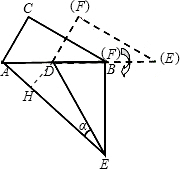
△BCD≌△BCF≌△EFB.
(3)过D点作DH⊥AE于H,在Rt△ABE中,AE= =
= ,
,
∵∠DAH=∠EAB,∠DHA=∠ABE=90°,
∴△ADH∽△AEB得 =
= ,即
,即 =
= ,解得DH=
,解得DH=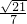 ,
,
而DE=AB=2,在Rt△DHE中,sin∠α=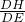 =
=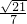 ÷2=
÷2=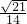 .
.
分析:(1)根据三角形全等和同底等高的三角形面积相等,找出面积相等的图形;
(2)根据全等三角形的判定定理解答;
(3)根据三角函数的概念解答.
点评:此题是一个动点问题,虽然图形发生了变化,但根据同底同底等高的三角形面积相等,找到面积相等的三角形.
所以四边形CDBF的面积不会变.
S四边形CDBF=S△ABC=
 ×2×
×2× =
= .
.(2)△COD≌△BOD≌△BOF≌△COF;
△ACD≌△FCD≌△BFD;

△BCD≌△BCF≌△EFB.
(3)过D点作DH⊥AE于H,在Rt△ABE中,AE=
 =
= ,
,∵∠DAH=∠EAB,∠DHA=∠ABE=90°,
∴△ADH∽△AEB得
 =
= ,即
,即 =
= ,解得DH=
,解得DH=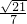 ,
,而DE=AB=2,在Rt△DHE中,sin∠α=
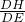 =
=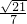 ÷2=
÷2=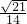 .
.分析:(1)根据三角形全等和同底等高的三角形面积相等,找出面积相等的图形;
(2)根据全等三角形的判定定理解答;
(3)根据三角函数的概念解答.
点评:此题是一个动点问题,虽然图形发生了变化,但根据同底同底等高的三角形面积相等,找到面积相等的三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
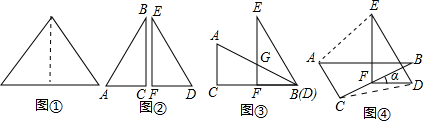
 如图,两个全等的Rt△ABC、Rt△EDC的直角顶点放置在一起,∠B=∠D=30°,AB与CD交于点M,ED与BC交于点N,AB与ED交于点F.
如图,两个全等的Rt△ABC、Rt△EDC的直角顶点放置在一起,∠B=∠D=30°,AB与CD交于点M,ED与BC交于点N,AB与ED交于点F.
 (2013•石景山区一模)如图,把两个全等的Rt△AOB和Rt△ECD分别置于平面直角坐标系xOy中,使点E与点B重合,直角边OB、BC在y轴上.已知点D (4,2),过A、D两点的直线交y轴于点F.若△ECD沿DA方向以每秒
(2013•石景山区一模)如图,把两个全等的Rt△AOB和Rt△ECD分别置于平面直角坐标系xOy中,使点E与点B重合,直角边OB、BC在y轴上.已知点D (4,2),过A、D两点的直线交y轴于点F.若△ECD沿DA方向以每秒