题目内容
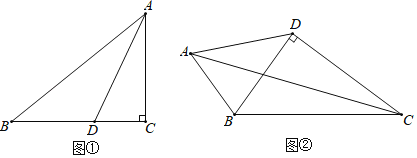
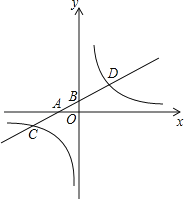
【题目】如图1,矩形ABCD中,AB=8,AD=6;点E是对角线BD上一动点,连接CE,作EF⊥CE交AB边于点F,以CE和EF为邻边作矩形CEFG,作其对角线相交于点H.

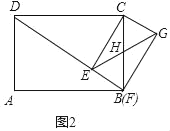
(1)如图2,当点F与点B重合时,求CE和CG的长;
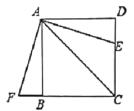
(2)如图3,当点E是BD中点时,求CE和CG的长;
(3)在图1,连接BG,当矩形CEFG随着点E的运动而变化时,猜想△EBG的形状?并加以证明.
【答案】(1)CE=![]() ,CG=
,CG=![]() ,(2)CE=5,CG=
,(2)CE=5,CG=![]() ;(3)结论:△EBG是直角三角形.理由见解析.
;(3)结论:△EBG是直角三角形.理由见解析.
【解析】
(1)利用面积法求出CE,再利用勾股定理求出EF即可;
(2)利用直角三角形斜边中线定理求出CE,再利用相似三角形的性质求出EF即可;
(3)根据直角三角形的判定方法:如果一个三角形一边上的中线等于这条边的一半,则这个三角形是直角三角形即可判断.
解:(1)如图2中,
在Rt△BAD中,BD=![]() =10,
=10,
∵S△BCD=![]() CDBC=
CDBC=![]() BDCE,
BDCE,
∴CE=![]() .CG=BE=
.CG=BE=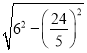 =
=![]() ,
,
(2)如图3中,过点E作MN⊥AM交AB于N,交CD于M.
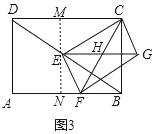
∵DE=BE,
∴CE=![]() BD=5,
BD=5,
∵△CME∽△ENF,
∴![]() ,
,
∴CG=EF=![]() .
.
(3)结论:△EBG是直角三角形.
理由:如图1中,连接BH.
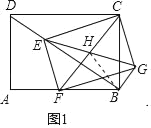
在Rt△BCF中,∵FH=CH,
∴BH=FH=CH,
∵四边形EFGC是矩形,
∴EH=HG=HF=HC,
∴BH=EH=HG,
∴△EBG是直角三角形.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目