题目内容
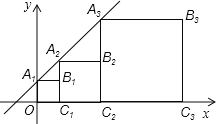
如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3…ln分别交于点A1,A2,A3,…An;函数y=2x的图象与直线l1,l2,l3…ln分别交于点B1,B2,B3…Bn,如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3…四边形An﹣1AnBnBn﹣1的面积记作Sn,那么S2014= _________ .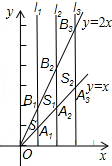
2013.5.
解析试题分析:根据直线解析式求出An-1Bn-1,AnBn的值,再根据直线ln-1与直线ln互相平行并判断出四边形An-1AnBn Bn-1是梯形,然后根据梯形的面积公式求出Sn的表达式,然后把n=2014代入表达式进行计算即可得解.
试题解析:根据题意,An-1Bn-1=2(n-1)-(n-1)=2n-2-n+1=n-1,
AnBn=2n-n=n,
∵直线ln-1⊥x轴于点(n-1,0),直线ln⊥x轴于点(n,0),
∴An-1Bn-1∥AnBn,且ln-1与ln间的距离为1,
∴四边形An-1AnBn Bn-1是梯形,
Sn= (n-1+n)×1=
(n-1+n)×1= (2n-1),
(2n-1),
当n=2014时,S2014= (2×2014-1)=2013.5.
(2×2014-1)=2013.5.
考点:一次函数图象上点的坐标特征.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
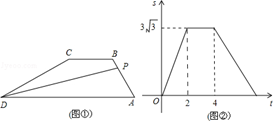
某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出的速度保持不变).该仓库库存物资m(吨)与时间t(小时)之间的函数关系如图所示.则这批物资从开始调进到全部调出所需要的时间是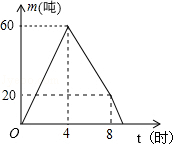
| A.8.4小时&nbs, | B.8.6小时&nbs, | C.8.8小时&nbs, | D.9小时&nbs, |

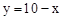 的图象与函数
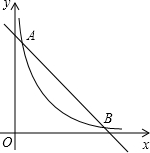
的图象与函数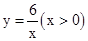 的图象相交于点A,B.设点A的坐标为(x1,y1),那么长为x1,宽为y1的矩形的面积为 ,周长为 .
的图象相交于点A,B.设点A的坐标为(x1,y1),那么长为x1,宽为y1的矩形的面积为 ,周长为 .