题目内容
【题目】如图1，在平面直角坐标系中，点O为坐标原点，直线
经过点
，且与x轴、y轴分别交于C，B两点．
求n的值；
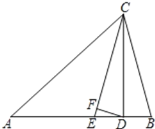
如图2，点D与点C关于y轴对称，点E在线段AB上，连接DE，过点E作
交y轴于点F，连接DF，若
，求点E的坐标；
如图3，在的条件下，点G在线段OD上，连接AG交DF于点M，点H在线段CG上，连接AH交DF于点N，若
，且
，求线段GH的长．
【答案】
n=5
；
8
【解析】
（1）把点
（6，8）代入直线
即可求出n的值.
（2）过点
分别作
轴、
轴的垂线，垂足分别为
，易证
≌
从而得出
，设设
，在
中，根据勾股定理列出方程求出t的值.从而得出点E的坐标.
（3）如图2，连接AD，延长
F交
于
，过
作
轴的平行线
，过作
于
，
作
于T，过Q作
轴于W.根据勾股定理列出方程，从而求出F点的坐标，再用待定系数法求出直线DF的解析式为：
，再与直线
联立组成方程组，求出交点的坐标，再利用全等三角形得到各条线段之间的关系，再次根据勾股定理列出方程求出各相关线段的长度，从而可证明四边形AMST是平行四边形，证明△AGH是等腰直角三角形可得结论．
解：把点
代入直线
中得，
，
分
；
分
如图1，过点E作
于K，
轴于P，
，
当
时，
，
，
，
点D与点C关于y轴对称，
，
分
在
和
中，
，
≌
，
，
分
点E在直线上，
设
，
，
四边形POKE是矩形，
，
在
中，
，
，
或10，
点E在线段AB上，
，
；
分
如图2，连接AD，延长DF交BC于Q，过A作x轴的平行线l，过Q作于R，过D作
于T，过Q作
轴于W，
令
，则
，
在
中，
，
，
，
，
分
设直线DF的解析式为：
，
，解得：
，
直线DF的解析式为：，
由
，解得：
，
；
可知
，
，
，
≌
，
，
，
，
，
，
分
在
中，
，
在
中，
，
，
，
，
，
，
，
将
绕点A逆时针旋转
得到
，连接
，
则≌，
，
，
，
，
，
，
≌
，
，
分
令
，则
，
，
，
在
中，
，
，
，
解得：
，
，
，
，
，
分
过点M作
于S，则
轴，
，
，
，
，
，
，
，
四边形AMST是平行四边形，
，
轴，
，
，
，
，
，
分
