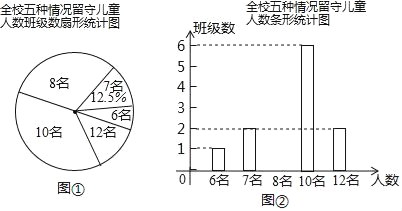
题目内容
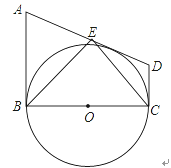
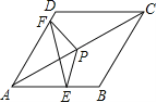
【题目】如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4,EF=4![]() ,∠BAD=60°,且AB>4
,∠BAD=60°,且AB>4![]() .
.
(1)求∠EPF的大小;
(2)若AP=6,求AE+AF的值.
【答案】(1)∠EPF=120°;(2)AE+AF=6![]() .
.
【解析】
试题分析: (1)过点P作PG⊥EF于G,解直角三角形即可得到结论;
(2)如图2,过点P作PM⊥AB于M,PN⊥AD于N,证明△ABC≌△ADC,Rt△PME≌Rt△PNF,问题即可得证.
试题解析:
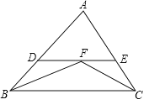
(1)如图1,过点P作PG⊥EF于G,
∵PE=PF,
∴FG=EG=![]() EF=2
EF=2![]() ,∠FPG=∠EPG=
,∠FPG=∠EPG=![]() ∠EPF,
∠EPF,
在△FPG中,sin∠FPG=![]() ,
,
∴∠FPG=60°,
∴∠EPF=2∠FPG=120°;
(2)如图2,过点P作PM⊥AB于M,PN⊥AD于N,
∵四边形ABCD是菱形,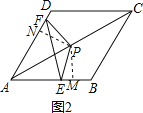
∴AD=AB,DC=BC,
∴∠DAC=∠BAC,
∴PM=PN,
在Rt△PME于Rt△PNF中,
![]() ,
,
∴Rt△PME≌Rt△PNF,
∴FN=EM,在Rt△PMA中,∠PMA=90°,∠PAM=![]() ∠DAB=30°,
∠DAB=30°,
∴AM=APcos30°=3![]() ,同理AN=3
,同理AN=3![]() ,
,
∴AE+AF=(AM-EM)+(AN+NF)=6![]() .
.

练习册系列答案
相关题目