题目内容
【题目】请选择一组你自己所喜欢的a，b，c的值，使二次函数y=ax2+bx+c（a≠0）的图象同时足下列条件：①开口向下，②当x＜﹣2时，y随x的增大而增大；当x＞﹣2时，y随x的增大而减小．这样的二次函数的解析式可以是________．
【答案】y=-x2+4x．（答案不唯一）.
【解析】
试题根据①的条件可知：a＜0；根据②的条件可知：抛物线的对称轴为x=2；满足上述条件的二次函数解析式均可．
试题解析：由①知：a＜0；
由②知：抛物线的对称轴为x=2；
可设抛物线的解析式为y=a（x-2）2+h（a＜0）；
当a=-1，h=4时，抛物线的解析式为y=-（x-2）2+4=-x2+4x．（答案不唯一）
练习册系列答案
相关题目
【题目】在一次课外学习中，小丁先画出图（1）所示的等边三角形，然后依次取各边中点并连接成图（2）、图（3）. 那么在第1个图形中有1个三角形，第2个图形中共有5个三角形，……，第n个图形中共有m个三角形．
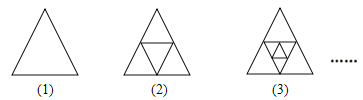
观察图形，填写下面的表格：
n | 1 | 2 | 3 | 4 | 5 | 6 | …… |
m | 1 | 5 |
（2）在研究的过程中，小丁发现，图形中三角形的总个数m与图形的序号n之间满足一次函数关系，试求出m与n的函数关系式，并指出自变量的取值范围.
（3）在进一步研究中小丁发现，当n＝
时，m的值与k的值有关，试直接写出m与k的关系式.
