题目内容
解下列方程:
(1)x2-4x+4=0;
(2)8y2-2=4y(配方法)
(3)x2-2x-2=0
(4)(2y-1)2=3(1-2y)
解:(1)(x-2)2=0,
∴x1=x2=2;
(2)8y2-4y=2,
y2- y=
y= ,
,
y2- y+
y+ =
=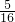 ,
,
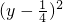 =
=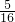 ,
,
y- =±
=±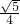 ,
,
∴y1=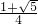 ,y2=
,y2=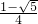 ;
;
(3)x2-2x=2,
x2-2x+1=3,
(x-1)2=3,
x-1=± ,
,
∴x1=1+ ,x2=1-
,x2=1- ;
;
(4)(2y-1)(2y-1+3)=0,
(2y-1)(2y+2)=0,
∴2y-1=0,2y+2=0,
解得y1= ,y2=-1.
,y2=-1.
分析:(1)用完全平方公式因式分解求出方程的根;
(2)用配方法解方程求出方程的根;
(3)用配方法解方程求出方程的根;
(4)把右边的项移到左边,用提公因式法因式分解求出方程的根.
点评:本题考查的是解一元二次方程,根据题目的结构特点和要求,选择适当的方法解方程,(1)题用完全平方公式解方程,(2)题按照题目的要求用配方法解方程,(3)用配方法解方程,(4)用提公因式法因式分解求出方程的根.
∴x1=x2=2;
(2)8y2-4y=2,
y2-
 y=
y= ,
,y2-
 y+
y+ =
=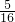 ,
,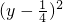 =
=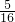 ,
,y-
 =±
=±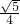 ,
,∴y1=
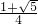 ,y2=
,y2=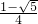 ;
;(3)x2-2x=2,
x2-2x+1=3,
(x-1)2=3,
x-1=±
 ,
,∴x1=1+
 ,x2=1-
,x2=1- ;
;(4)(2y-1)(2y-1+3)=0,
(2y-1)(2y+2)=0,
∴2y-1=0,2y+2=0,
解得y1=
 ,y2=-1.
,y2=-1.分析:(1)用完全平方公式因式分解求出方程的根;
(2)用配方法解方程求出方程的根;
(3)用配方法解方程求出方程的根;
(4)把右边的项移到左边,用提公因式法因式分解求出方程的根.
点评:本题考查的是解一元二次方程,根据题目的结构特点和要求,选择适当的方法解方程,(1)题用完全平方公式解方程,(2)题按照题目的要求用配方法解方程,(3)用配方法解方程,(4)用提公因式法因式分解求出方程的根.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目