题目内容
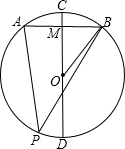 如图,在⊙O中,CD是直径,AB是弦,AB⊥CD于M,P是弧AD上任一点,CD=20,CM=4.
如图,在⊙O中,CD是直径,AB是弦,AB⊥CD于M,P是弧AD上任一点,CD=20,CM=4.(1)求弦AB的长;
(2)求证:∠APB=∠COB.
分析:(1)在直角△OBM中,根据勾股定理即可求得BM的长,则AB=2BM,即可求解;
(2)根据同弧所对的圆周角等于同弧所对圆心角的一半即可求解.
(2)根据同弧所对的圆周角等于同弧所对圆心角的一半即可求解.
解答:解:(1)∵CD是直径,且CD=20,
∴OB=OC=10.
∵AB⊥CD,∴BM=
AB.
在Rt△BMO中,OM=10-CM=6,OB=10,由勾股定理可得,BM=
=8,(2分)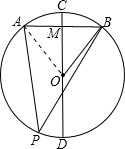
∴AB=16.(3分)
(2)连接OA,∵AB⊥CD,
∴弧AC=弧BC.
∴∠AOC=∠BOC=
∠BOA.(5分)
∵∠APB=
∠BOA,
∴∠APB=∠BOC.(6分)
∴OB=OC=10.
∵AB⊥CD,∴BM=
| 1 |
| 2 |
在Rt△BMO中,OM=10-CM=6,OB=10,由勾股定理可得,BM=
| 102-62 |

∴AB=16.(3分)
(2)连接OA,∵AB⊥CD,
∴弧AC=弧BC.
∴∠AOC=∠BOC=
| 1 |
| 2 |
∵∠APB=
| 1 |
| 2 |
∴∠APB=∠BOC.(6分)
点评:此题涉及圆中求半径的问题,此类在圆中涉及弦长、半径、圆心角的计算的问题,常把半弦长,半圆心角,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形予以求解,常见辅助线是过圆心作弦的垂线.

练习册系列答案
相关题目
 13、如图,在△ABC中,CD是AB边上的中线,线段AC比BC短2cm,则△BCD和△ACD的周长的差是
13、如图,在△ABC中,CD是AB边上的中线,线段AC比BC短2cm,则△BCD和△ACD的周长的差是 14、如图,在△ABC中,CD平分∠ACB,DE∥AC,DC∥EF,则与∠ACD相等角有
14、如图,在△ABC中,CD平分∠ACB,DE∥AC,DC∥EF,则与∠ACD相等角有
 如图,在△ABC中,CD、BE分别是AB、AC边上的高,∠EBC=45°,BE=6,CD=
如图,在△ABC中,CD、BE分别是AB、AC边上的高,∠EBC=45°,BE=6,CD=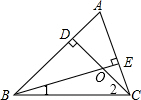 如图,在△ABC中,CD是AB边上的高,BE是AC边上的高,点O是两条高线的交点,则∠A与∠1+∠2的关系是( )
如图,在△ABC中,CD是AB边上的高,BE是AC边上的高,点O是两条高线的交点,则∠A与∠1+∠2的关系是( ) 如图,在⊙O中,
如图,在⊙O中,