题目内容
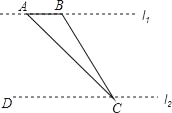
【题目】如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为S1、S2、S3,若S1=4,S3=12,则S2的值为( )

A.16B.24C.48D.64
【答案】D
【解析】
根据已知条件得到AB=2,CD=2![]() ,过A作AE∥CD交BC于E,则∠AEB=∠DCB,根据平行四边形的性质得到CE=AD,AE=CD=2
,过A作AE∥CD交BC于E,则∠AEB=∠DCB,根据平行四边形的性质得到CE=AD,AE=CD=2![]() ,由已知条件得到∠BAE=90°,根据勾股定理得到BE=
,由已知条件得到∠BAE=90°,根据勾股定理得到BE=![]() ,于是得到结论.
,于是得到结论.
解:∵S1=4,S3=12,
∴AB=2,CD=2![]() ,
,
过A作AE∥CD交BC于E,

则∠AEB=∠DCB,
∵AD∥BC,
∴四边形AECD是平行四边形,
∴CE=AD,AE=CD=2![]() ,
,
∵∠ABC+∠DCB=90°,
∴∠AEB+∠ABC=90°,
∴∠BAE=90°,
∴BE=![]() ,
,
∵BC=2AD,
∴BC=2BE=8,
∴S2=(8)2=64,
故选:D.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目