题目内容
 (2013•东阳市模拟)如图,C、D、B的坐标分别为(1,0)(9,0)(10,0),点P(t,0)是CD上一个动点,在x轴上方作等边△OPE和△BPF,连EF,G为EF的中点.
(2013•东阳市模拟)如图,C、D、B的坐标分别为(1,0)(9,0)(10,0),点P(t,0)是CD上一个动点,在x轴上方作等边△OPE和△BPF,连EF,G为EF的中点.(1)当t=
5
5
时,EF∥OB;(2)双曲线y=
| k |
| x |
| ||
| 2 |
10
或15
| 3 |
| 3 |
10
或15
.| 3 |
| 3 |
分析:(1)作EM⊥OB于M点,FN⊥OB于N点,根据等边三角形的性质得EM=
OP,FN=
PB,所以EM=FN时,EF∥OB,则
t=
(10-t),然后即方程即可得到t的值;
(2)作GH⊥OB于H点,则GH为梯形EMNF的中位线,根据梯形中位线的性质得GH=
(EM+FN)=
,HM=
MN=
(ON-OM)=
,得到PH=
-
t或
t-
,
再利用勾股定理得PG2=GH2+PH2,即(
)2+(
)2=(
)2,解得t1=3,t2=7,然后分别确定G点坐标,再代入反比例函数解析式可得到k的值.,
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(2)作GH⊥OB于H点,则GH为梯形EMNF的中位线,根据梯形中位线的性质得GH=
| 1 |
| 2 |
5
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
再利用勾股定理得PG2=GH2+PH2,即(
5
| ||
| 2 |
| 5-t |
| 2 |
| ||
| 2 |
解答:解:(1)作EM⊥OB于M点,FN⊥OB于N点,如图,
∵△OPE和△BPF都是等边三角形,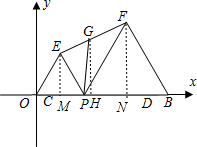
∴EM=
OP,FN=
PB,
当EM=FN时,EF∥OB,
∵P(t,0),B(10,0),
∴PO=t,PB=10-t
∴
t=
(10-t),
∴t=5;
(2)作GH⊥OB于H点,如图,
∵G为EF的中点,
∴GH为梯形EMNF的中位线,
∴GH=
(EM+FN)=
[
t+
(10-t)]=
,HM=
MN=
(ON-OM)=
[t+
(10-t)-
t]=
,
∴PH=
-
t或
t-
,
在Rt△PGH中,PG2=GH2+PH2,
∴(
)2+(
)2=(
)2,
∴t1=3,t2=7,
当t=3时,OH=
+
t=4,
∴G点坐标为(4,
),
把G(4,
)代入y=
得k=4×
=10
;
当t=7时,OH=
+
=6,
∴G点坐标为(6,
),
把G(6,
)代入y=
得k=6×
=15
;
∴k的值为10
或15
.
故答案为5;10
或15
.
∵△OPE和△BPF都是等边三角形,

∴EM=
| ||
| 2 |
| ||
| 2 |
当EM=FN时,EF∥OB,
∵P(t,0),B(10,0),
∴PO=t,PB=10-t
∴
| ||
| 2 |
| ||
| 2 |
∴t=5;
(2)作GH⊥OB于H点,如图,
∵G为EF的中点,
∴GH为梯形EMNF的中位线,
∴GH=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
5
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴PH=
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
在Rt△PGH中,PG2=GH2+PH2,
∴(
5
| ||
| 2 |
| 5-t |
| 2 |
| ||
| 2 |
∴t1=3,t2=7,
当t=3时,OH=
| 5 |
| 2 |
| 1 |
| 2 |
∴G点坐标为(4,
5
| ||
| 2 |
把G(4,
5
| ||
| 2 |
| k |
| x |
5
| ||
| 2 |
| 3 |
当t=7时,OH=
| 5 |
| 2 |
| t |
| 2 |
∴G点坐标为(6,
5
| ||
| 2 |
把G(6,
5
| ||
| 2 |
| k |
| x |
5
| ||
| 2 |
| 3 |
∴k的值为10
| 3 |
| 3 |
故答案为5;10
| 3 |
| 3 |
点评:本题考查了反比例函数的综合题:反比例函数图象上点的坐标满足其函数解析式,运用待定系数法求函数的解析式;掌握等边三角形的性质、含30°的直角三角形三边的关系和勾股定理.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
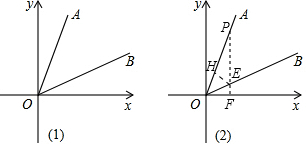
 (2013•东阳市模拟)如图,平面直角坐标系中,点A(0,4),B(3,0),D、E在x轴上,F为平面上一点,且EF⊥x轴,直线DF与直线AB互相垂直,垂足为H,△AOB≌△DEF,设BD=h.
(2013•东阳市模拟)如图,平面直角坐标系中,点A(0,4),B(3,0),D、E在x轴上,F为平面上一点,且EF⊥x轴,直线DF与直线AB互相垂直,垂足为H,△AOB≌△DEF,设BD=h.