题目内容
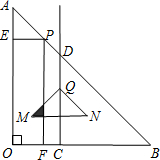 (2012•长春一模)如图,在△AOB中,∠AOB=90°,OA=OB=6,C为OB上一点,射线CD⊥OB交AB于点D,OC=2.点P从点A出发以每秒
(2012•长春一模)如图,在△AOB中,∠AOB=90°,OA=OB=6,C为OB上一点,射线CD⊥OB交AB于点D,OC=2.点P从点A出发以每秒| 2 |
(1)求t=1时FC的长度.
(2)求MN=PF时t的值.
(3)当△QMN和矩形PEOF有重叠部分时,求重叠(阴影)部分图形面积S与t的函数关系式.
(4)直接写出△QMN的边与矩形PEOF的边有三个公共点时t的值.
分析:(1)根据等腰直角三角形,可得AP=
t,OF=EP=t,再将t=1代入求出FC的长度;
(2)根据MN=PF,可得关于t的方程6-t=2t,解方程即可求解;
(3)分三种情况:求出当1≤t≤2时;当2<t≤
时;当
<t≤3时;求出重叠(阴影)部分图形面积S与t的函数关系式;
(4)分M在OE上;N在PF上两种情况讨论求得△QMN的边与矩形PEOF的边有三个公共点时t的值.
| 2 |
(2)根据MN=PF,可得关于t的方程6-t=2t,解方程即可求解;
(3)分三种情况:求出当1≤t≤2时;当2<t≤
| 8 |
| 3 |
| 8 |
| 3 |
(4)分M在OE上;N在PF上两种情况讨论求得△QMN的边与矩形PEOF的边有三个公共点时t的值.
解答:解:(1)根据题意,△AOB、△AEP都是等腰直角三角形.
∵AP=
t,OF=EP=t,
∴当t=1时,FC=1;
(2)∵AP=
t,AE=t,PF=OE=6-t
MN=QC=2t
∴6-t=2t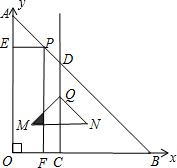
解得t=2.
故当t=2时,MN=PF;
(3)当1≤t≤2时,S=2t2-4t+2;
当2<t≤
时,S=-
t2+30t-32;
当
<t≤3时,S=-2t2+6t;
(4)建立如图所示的平面直角坐标系.
设经过t秒△QMN的边与矩形PEOF的边有三个公共点,即点M在OA上,
当点P在AD的左侧时,设经过t秒△QMN的边与矩形PEOF的边有三个公共点,
∵AP=
t,∠A=45°,PE⊥AB,
∴PE=t,CQ=2t,
∵MN=CQ,△MNQ是等腰直角三角形,C(2,0)
∴t=2时,△QMN的边与矩形PEOF的边有三个公共点;
当点P在AD的右侧时,设经过t秒△QMN的边与矩形PEOF的边有三个公共点,
此时,PE=t,6-t=2t-2,解得t=
,
∴△QMN的边与矩形PEOF的边有三个公共点时t=2或
.
∵AP=
| 2 |
∴当t=1时,FC=1;
(2)∵AP=
| 2 |
MN=QC=2t
∴6-t=2t

解得t=2.
故当t=2时,MN=PF;
(3)当1≤t≤2时,S=2t2-4t+2;
当2<t≤
| 8 |
| 3 |
| 13 |
| 2 |
当
| 8 |
| 3 |
(4)建立如图所示的平面直角坐标系.
设经过t秒△QMN的边与矩形PEOF的边有三个公共点,即点M在OA上,
当点P在AD的左侧时,设经过t秒△QMN的边与矩形PEOF的边有三个公共点,
∵AP=
| 2 |
∴PE=t,CQ=2t,
∵MN=CQ,△MNQ是等腰直角三角形,C(2,0)
∴t=2时,△QMN的边与矩形PEOF的边有三个公共点;
当点P在AD的右侧时,设经过t秒△QMN的边与矩形PEOF的边有三个公共点,
此时,PE=t,6-t=2t-2,解得t=
| 8 |
| 3 |
∴△QMN的边与矩形PEOF的边有三个公共点时t=2或
| 8 |
| 3 |
点评:考查了相似形综合题,涉及的知识有等腰直角三角形的性质,图形的面积计算,函数思想,方程思想,分类思想的运用,有一定的难度.

练习册系列答案
相关题目
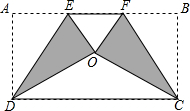 (2012•长春一模)将矩形纸片ABCD按如图方式折叠,DE、CF为折痕,折叠后点A和点B都落在点O处.若△EOF是等边三角形,则
(2012•长春一模)将矩形纸片ABCD按如图方式折叠,DE、CF为折痕,折叠后点A和点B都落在点O处.若△EOF是等边三角形,则 (2012•长春一模)如图,抛物线y=ax2-x-
(2012•长春一模)如图,抛物线y=ax2-x- -B于点P,以PQ为一边向右作正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形OABC重叠面积为S(平方单位)
-B于点P,以PQ为一边向右作正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形OABC重叠面积为S(平方单位)