��Ŀ����
����Ŀ����֪��ͬѧ���в������ŷֱ�������� ![]() ��
�� ![]() ��1�Ŀ�Ƭ����ͬѧ���в������ŷֱ����1��3��2�Ŀ�Ƭ����Ƭ������ͬ���ִӼ����������и���ȡһ�ſ�Ƭ���������ǵ����ֱַ��Ϊa��b��
��1�Ŀ�Ƭ����ͬѧ���в������ŷֱ����1��3��2�Ŀ�Ƭ����Ƭ������ͬ���ִӼ����������и���ȡһ�ſ�Ƭ���������ǵ����ֱַ��Ϊa��b��
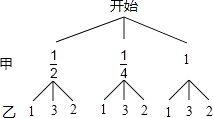
��1������������ͼ���б����г����п��ܵĽ����
��2�����ƶ�����һ����Ϸ��������ѡ����a��b��ʹ��ax2+bx+1=0����������ȵ�ʵ��������Ƽ�ʤ��������һ�ʤ��������������Ϸ����ƽ�������ø���֪ʶ���ͣ�
���𰸡�
��1���⣺����״ͼ�ã�
�ߣ�a��b���Ŀ��ܽ���У� ![]() ��1������
��1������ ![]() ��3������
��3������ ![]() ��2������
��2������ ![]() ��1������
��1������ ![]() ��3������
��3������ ![]() ��2������1��1������1��3������1��2����
��2������1��1������1��3������1��2����
�ࣨa��b��ȡֵ�������9�֣�
��2���⣺�ߵ�a= ![]() ��b=1ʱ����=b2��4ac=��1��0����ʱax2+bx+1=0��ʵ������
��b=1ʱ����=b2��4ac=��1��0����ʱax2+bx+1=0��ʵ������
��a= ![]() ��b=3ʱ����=b2��4ac=7��0����ʱax2+bx+1=0����������ȵ�ʵ������
��b=3ʱ����=b2��4ac=7��0����ʱax2+bx+1=0����������ȵ�ʵ������
��a= ![]() ��b=2ʱ����=b2��4ac=2��0����ʱax2+bx+1=0����������ȵ�ʵ������
��b=2ʱ����=b2��4ac=2��0����ʱax2+bx+1=0����������ȵ�ʵ������
��a= ![]() ��b=1ʱ����=b2��4ac=0����ʱax2+bx+1=0��������ȵ�ʵ������
��b=1ʱ����=b2��4ac=0����ʱax2+bx+1=0��������ȵ�ʵ������
��a= ![]() ��b=3ʱ����=b2��4ac=8��0����ʱax2+bx+1=0����������ȵ�ʵ������
��b=3ʱ����=b2��4ac=8��0����ʱax2+bx+1=0����������ȵ�ʵ������
��a= ![]() ��b=2ʱ����=b2��4ac=3��0����ʱax2+bx+1=0����������ȵ�ʵ������
��b=2ʱ����=b2��4ac=3��0����ʱax2+bx+1=0����������ȵ�ʵ������
��a=1��b=1ʱ����=b2��4ac=��3��0����ʱax2+bx+1=0��ʵ������
��a=1��b=3ʱ����=b2��4ac=5��0����ʱax2+bx+1=0����������ȵ�ʵ������
��a=1��b=2ʱ����=b2��4ac=0����ʱax2+bx+1=0��������ȵ�ʵ������
��P����ʤ��=P������0��= ![]() ��P���һ�ʤ��=
��P���һ�ʤ��= ![]() ��
��
����������Ϸ����Լ�����������ƽ��
����������1�����ȸ������⻭����״ͼ��Ȼ�������״ͼ����������еȿ��ܵĽ������2������һԪ���η��̸����б�ʽ�������ж���������¸��������Ȼ�����ø��ʹ�ʽ��⼴����üס��һ�ʤ�ĸ��ʣ��Ƚϸ��ʴ�С������ȷ����������Ϸ���Ƿ�ƽ��
�����㾫�������ڱ��⿼��������ʽ���б�������״ͼ������Ҫ�˽�����б�ʽ��=b2-4ac��������Է�Ϊ3�������1������>0ʱ��һԪ���η�����2������ȵ�ʵ����2������=0ʱ��һԪ���η�����2����ͬ��ʵ����3������<0ʱ��һԪ���η���û��ʵ��������һ������Ҫ�����������������ʱ�����б����Ͳ������ˣ�Ϊ�˲��ز�©���г����п��ܵĽ����ͨ��������״ͼ������ʲ��ܵó���ȷ�𰸣�

 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�����Ŀ��һ�������A�س�������һ����������Ľֵ���������ÿ����ʻ�����������Ϊ������¼���£�x��5��x��14����λ��m����
��ʻ���� | ��һ�� | �ڶ��� | ������ | ���Ĵ� |
��ʻ��� | x | �� | x��3 | 2��5��x�� |
��ʻ���������������������� | �� �� | �� �� | �� �� | �� �� |
��1���뽫����������
��2��������4����ʻ������������ڵ�λ�ã�
��3���������ʻ����·��Ϊ41m�����һ����ʻ��·��x��ֵ��
����Ŀ��ijУΪ�˸��õĿ�չ��ѧУ��ɫ��������������ȫУ���꼶���������ȡ��60ѧ�������и���������Ŀ�IJ��ԣ��˽����ǵ���������������±��������������ݣ��õ��Ĺ���ÿ������IJ��Գɼ��IJ���ͳ�Ʊ���ͼ�� ijУ60��ѧ���������Գɼ��ɼ�ͳ�Ʊ�
�ɼ� | ���� | Ƶ�� | Ƶ�� |
���� | ������ | a | 0.3 |
���� | ������������ | 30 | b |
�ϸ� | �� | 9 | 0.15 |
���ϸ� |
| c | d |
�ϼ� |
��˵����40��55��Ϊ���ϸ�55��70��Ϊ�ϸ�70��85��Ϊ���ã�85��100��Ϊ���㣩
�����������Ϣ������������⣺
��1�����е�a=��b=��c=��d= ��
��2�������Ƶ���ֲ�����������Ӧ��Ƶ���ֲ�ֱ��ͼ��




