Question

【题目】）如图，点A（m，6），B（n，1）在反比例函数图象上，AD⊥x轴于点D，BC⊥x轴于点C，DC=5．
（1）求m，n的值并写出反比例函数的表达式；
（2）连接AB，E是线段AB上一点，过点E作x轴的垂线，交反比例函数图象于点F，若EF=AD，求出点E的坐标．

Answer 1

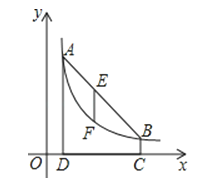
【答案】解：（1）设反比例函数的解析式为y=，
把（n，1）代入得：k=n，
即y=，
∵点A（m，6），B（n，1）在反比例函数图象上，AD⊥x轴于点D，BC⊥x轴于点C，DC=5，
∴，
解得：m=1，n=6，
即A（1，6），B（6，1）；
反比例函数的解析式为：y=；
（2）设直线AB的解析式为y=ax+b，
把A（1，6）和B（6，1）代入得：
解得：a=﹣1，b=7，
即直线AB的解析式为：y=﹣x+7，
设E点的横坐标为m，则E（m，﹣m+7），F（m，），
∴EF=﹣m+7﹣，
∵EF=AD，
∴﹣m+7﹣=，
解得：m=2，m2=3，
经检验都是原方程的解，
即E的坐标为（2，5）或（3，4）．
【解析】（1）设反比例函数的解析式为y= ， 根据题意得出方程组 ， 求出方程组的解即可；
（2）设直线AB的解析式为y=ax+b，求出直线AB的解析式，设E点的横坐标为m，则E（m，﹣m+7），F（m，），求出EF=﹣m+7﹣ ， 得出关于m的方程，求出m即可．