题目内容
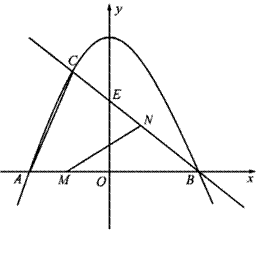
已知:如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点A、B,点A的坐标为(4,0)
轴交于点A、B,点A的坐标为(4,0)
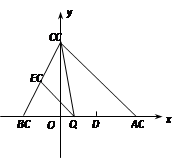
1.求该抛物线的解析式;
2.点Q是线段AB上的动点,过点Q作QE//AC,交BC于点E,连接CQ,设△CQE的面积为S,Q(m,0),试求S与m之间的函数关系式(写出自变量m的取值范围);
3.在(2)的条件下,当△CQE的面积最大时,求点E的坐标.
4.若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0). 问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标,若不存在,请说明理由.
1.![]()
2.设点Q坐标为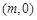 ,过点
,过点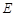 作EG⊥x轴于G,由
作EG⊥x轴于G,由 得
得 ,
,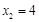
∴点B的坐标为![]() ,点A的坐标为
,点A的坐标为![]()
∴AB=6 BQ=m+2 ∵QE//AC ∴△BQE∽△BAC 又△BEG∽△BCO
∴![]() 即
即![]() ∴
∴![]()
∴![]()
![]()
即![]()
3.由(2)知![]()
又![]()
![]() ∴当
∴当![]() 时 S最大
时 S最大
此时![]() BQ=QA 又QE//CA
BQ=QA 又QE//CA
∴BE=EC ∴点E为BC的中点,∴![]()
4.存在,在△ODF中
①若DO=DF ∵A(4,0) D(2,0) ∴AD=OD=DF=2
又在Rt△AOC中,OA=OC=4 ∴∠OAC=45°∴∠DFA=∠OAC=45°
∴∠ADF=90°,此时,点F的坐标为(2, 2)
由![]() 得
得![]()
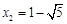 ,此时点P的坐标为:
,此时点P的坐标为:
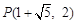 或
或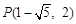
②若FO=FD,过点F作FM⊥x轴于点M,由等腰三角形的性质得
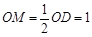 ∴AM=3 ∴在等腰直角△AMF中
∴AM=3 ∴在等腰直角△AMF中
MF=AM=3 ∴F(1,3) 由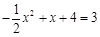
得![]()
![]() 此时,点P的坐标为
此时,点P的坐标为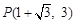 或
或
③若OD=OF ∵OA=OC=4 且∠AOC=90° ∴AC=4![]()
∴点O到AC的距离为![]() ,而OF=OD=2∠
,而OF=OD=2∠![]() ,此时,不存在这样的直线l,
,此时,不存在这样的直线l,
使得△ODF是等腰三角形
综上,存在满足条件的点![]() 或
或![]() 或
或![]() 或
或![]()
解析:
1.根据A,C两点坐标,利用待定系数法求二次函数解析式即可;
2.根据△ABC与△ABM的面积相等,得出M的纵坐标为:±4,进而得出x的值即可;
3.利用相似三角形的性质得出S△CQE=![]() x×4-
x×4-![]() x2=-
x2=-![]() x2+2x,进而求出即可;
x2+2x,进而求出即可;
4.利用图象以及等腰三角形的性质假设若DO=DF时以及当FO=FD和当DF=OD时分别得出F点的坐标,将纵坐标代入二次函数解析式即可求出P点坐标.

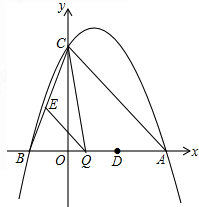 (2012•浦江县模拟)已知:如图,抛物线与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0),点B的坐标为(-2,0).
(2012•浦江县模拟)已知:如图,抛物线与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0),点B的坐标为(-2,0).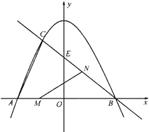
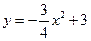 与
与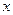 轴交于点
轴交于点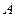 、点
、点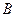 ,与直线
,与直线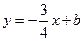 相交于点
相交于点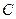 ,直线
,直线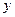 轴交于点
轴交于点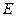 。
。
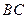 的解析式;
的解析式;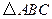 的面积;
的面积;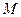 在线段
在线段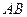 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从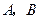 重合),同时,点
重合),同时,点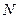 在射线
在射线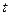 秒,请写出
秒,请写出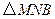 的面积
的面积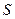 与
与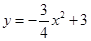 与
与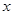 轴交于点
轴交于点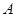 ,点
,点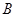 ,与直线
,与直线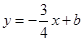 相交于点
相交于点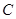 ,直线
,直线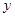 轴交于点
轴交于点 .
.
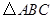 的面积.
的面积.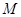 在线段
在线段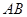 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从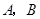 重合),同时,点
重合),同时,点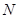 在射线
在射线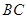 上以每秒2个单位长度的速度从
上以每秒2个单位长度的速度从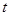 秒,请写出
秒,请写出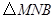 的面积
的面积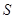 与
与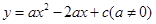 与
与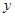 轴交于点
轴交于点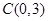 ,与
,与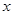 轴交于
轴交于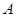 、
、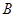 两点,点
两点,点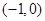 .
.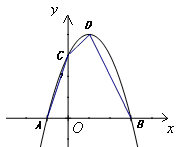
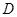 的坐标;
的坐标;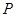 是在第一象限内抛物线上的一个动点,求使与四边形
是在第一象限内抛物线上的一个动点,求使与四边形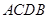 面积相等的四边形
面积相等的四边形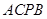 的点
的点 的面积.
的面积.