题目内容
已知:如图,抛物线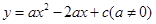 与
与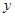 轴交于点
轴交于点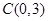 ,与
,与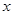 轴交于
轴交于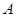 、
、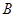 两点,点
两点,点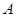 的坐标为
的坐标为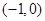 .
.
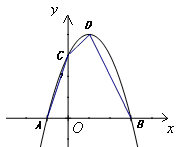
(1)求抛物线的解析式及顶点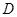 的坐标;
的坐标;
(2)设点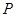 是在第一象限内抛物线上的一个动点,求使与四边形
是在第一象限内抛物线上的一个动点,求使与四边形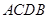 面积相等的四边形
面积相等的四边形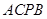 的点
的点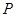 的坐标;
的坐标;
(3)求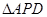 的面积.
的面积.
【答案】
解:(1)∵抛物线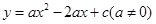 与
与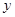 轴交于点
轴交于点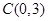 ,与
,与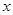 轴
轴
交于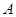
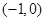
∴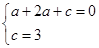 解得
解得 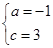
∴ 抛物线的解析式为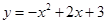 ----------------1分
----------------1分
∵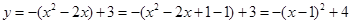
∴顶点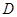 的坐标为( 1 ,4) -----------------2分
的坐标为( 1 ,4) -----------------2分
(2)连结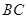 ,过点D作
,过点D作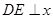 轴于点
轴于点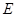 .
.
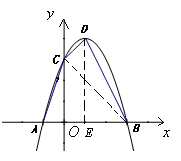
令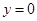 则
则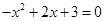
∴ 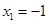 ,
,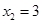
∴ 点B的坐标为(3 ,0
∴
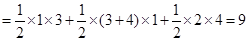 --------3分
--------3分
∵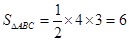
∴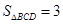
∵点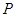 是在第一象限内抛物线上的一个动点,
是在第一象限内抛物线上的一个动点,
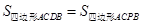
∴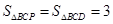
∴ 点P 是过 D 且与直线BC平行的直线和抛物线的交点
而直线BC的函数解析式为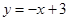 --------------------4分
--------------------4分
∴设直线DP的函数解析式为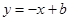 , 过点D(1,4)
, 过点D(1,4)
∴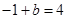 ,
, 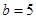
∴直线DP的函数解析式为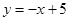 ----------------------5分
----------------------5分
把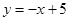 代入
代入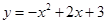 中,解得
中,解得 ,
,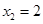
∴点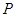 的坐标为(2,3) ---------------------------------6分
的坐标为(2,3) ---------------------------------6分
(3)∵点P 与点C关于DE 对称,点B与点A关于 DE 对称
∴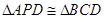
∴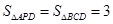 .---------------7分
.---------------7分
【解析】略

练习册系列答案
相关题目
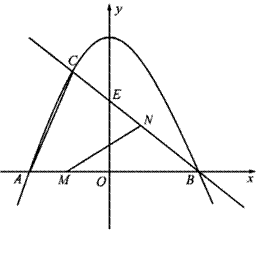
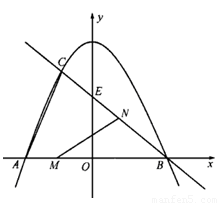
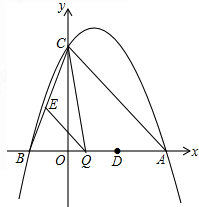 (2012•浦江县模拟)已知:如图,抛物线与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0),点B的坐标为(-2,0).
(2012•浦江县模拟)已知:如图,抛物线与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0),点B的坐标为(-2,0).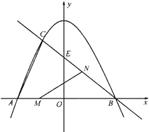
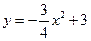 与
与 轴交于点
轴交于点 、点
、点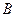 ,与直线
,与直线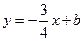 相交于点
相交于点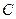 ,直线
,直线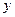 轴交于点
轴交于点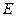 。
。
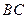 的解析式;
的解析式;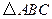 的面积;
的面积;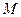 在线段
在线段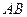 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从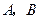 重合),同时,点
重合),同时,点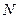 在射线
在射线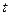 秒,请写出
秒,请写出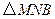 的面积
的面积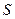 与
与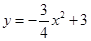 与
与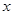 轴交于点
轴交于点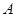 ,点
,点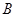 ,与直线
,与直线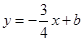 相交于点
相交于点 ,直线
,直线 轴交于点
轴交于点 .
.
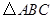 的面积.
的面积.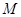 在线段
在线段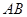 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从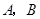 重合),同时,点
重合),同时,点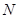 在射线
在射线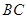 上以每秒2个单位长度的速度从
上以每秒2个单位长度的速度从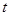 秒,请写出
秒,请写出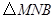 的面积
的面积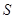 与
与