题目内容
已知关于x的一元二次方程x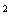 +4x+m=O.
+4x+m=O.
(1)当m=l时,请用配方法求方程的根:
(2)若方程没有实数根,求m的取值范围.
【答案】
(1) x=-2±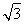 ;m>4.
;m>4.
【解析】
试题分析:(1)先把m=1代入已知方程,然后将常数项1移到等式的右边,再在等式的两边同时加上一次项系数一半的平方;
(2)当方程无实数根时,根的判别式小于零列出关于k的不等式,通过解不等式即可求得m的取值范围.
试题解析:(1)当m=1时,x2+4x+1=0,
∴x2+4x+4=3,
∴(x+2)2=3,
∴x+2=±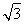 ,
,
∴x=-2±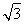 ;
;
(2)∵x2+4x+m=O,
∴42-4m<0,
∴m>4.
考点: 1.根的判别式;2.解一元二次方程-配方法.

练习册系列答案
相关题目
已知关于x的一元二次x2-6x+k+1=0的两个实数根x1,x2,
+
=1,则k的值是( )
| 1 |
| x1 |
| 1 |
| x2 |
| A、8 | B、-7 | C、6 | D、5 |
 .
. .
.