题目内容
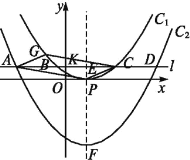
【题目】如图,A(﹣1,0),B(4,0),C(0,3)三点在抛物线y=ax2+bx+c上,D为直线BC上方抛物线上一动点,E在CB上,∠DEC=90°
(1)求抛物线的函数表达式;
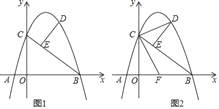
(2)如图1,求线段DE长度的最大值;
(3)如图2,F为AB的中点,连接CF,CD,当△CDE中有一个角与∠CFO相等时,求点D的横坐标;若不存在,请说明理由.
【答案】(1)y=![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)根据待定系数法,可得函数解析式;
(2)根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得DM,根据相似三角形的判定与性质,可得DE的长,根据二次函数的性质,可得答案;
(3)根据正切函数,可得∠CFO,根据相似三角形的性质,可得GH,BH,根据待定系数法,可得CG的解析式,根据解方程组,可得答案.
解:(1)由题意,得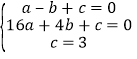 ,
,
解得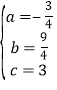 ,
,
抛物线的函数表达式为y=﹣![]() x2+
x2+![]() x+3;
x+3;
(2)设直线BC的解析是为y=kx+b,![]() ,
,
解得 ,
,
∴y=﹣![]() x+3,
x+3,
设D(a,﹣![]() a2+
a2+![]() a+3),(0<a<4),过点D作DM⊥x轴交BC于M点,
a+3),(0<a<4),过点D作DM⊥x轴交BC于M点,
如图1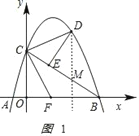 ,
,
M(a,﹣![]() a+3),
a+3),
DM=(﹣![]() a2+
a2+![]() a+3)﹣(﹣
a+3)﹣(﹣![]() a+3)=﹣
a+3)=﹣![]() a2+3a,
a2+3a,
∵∠DME=∠OCB,∠DEM=∠BOC,
∴△DEM∽△BOC,
∴![]() ,
,
∵OB=4,OC=3,
∴BC=5,
∴DE=![]() DM
DM
∴DE=﹣![]() a2+
a2+![]() a=﹣
a=﹣![]() (a﹣2)2+
(a﹣2)2+![]() ,
,
当a=2时,DE取最大值,最大值是![]() ,
,
(3)假设存在这样的点D,使得△CDE中有一个角与∠CFO相等,
∵点F为AB的中点,
∴OF=![]() ,tan∠CFO=
,tan∠CFO=![]() =2,
=2,
过点B作BG⊥BC,交CD的延长线于G点,过点G作GH⊥x轴,垂足为H,
如图2
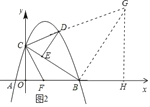 ,
,
①若∠DCE=∠CFO,
∴tan∠DCE=![]() =2,
=2,
∴BG=10,
∵△GBH∽BCO,
∴![]() ,
,
∴GH=8,BH=6,
∴G(10,8),
设直线CG的解析式为y=kx+b,
∴![]() ,
,
解得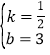 ,
,
∴直线CG的解析式为y=![]() x+3,
x+3,
∴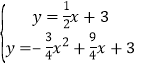 ,
,
解得x=![]() ,或x=0(舍).
,或x=0(舍).
②若∠CDE=∠CFO,
同理可得BG=![]() ,GH=2,BH=
,GH=2,BH=![]() ,
,
∴G(![]() ,2),
,2),
同理可得,直线CG的解析是为y=﹣![]() x+3,
x+3,
∴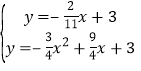 ,
,
解得x=![]() 或x=0(舍),
或x=0(舍),
综上所述,存在点D,使得△CDE中有一个角与∠CFO相等,点D的横坐标为![]() 或
或![]() .
.

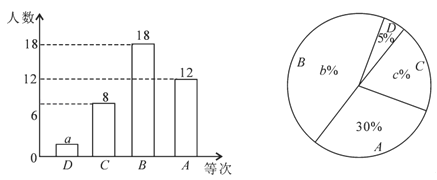
【题目】某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
(1)则样本容量是 ,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12的次数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |