题目内容
已知:如图,Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,且不与A、B两点重合,AE⊥AB,AE=BD,连接DE、DC.
(1)求证:△ACE≌△BCD;
(2)猜想:△DCE是 三角形;并说明理由.
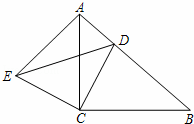
(1)证明:
∵∠ACB=90°,AC=BC,
 ∴∠B=∠2=45°.
∴∠B=∠2=45°.
∵AE⊥AB,
∴∠1+∠2=90°.
∴∠1=45°.
∴∠1=∠B.
![]() 在△ACE和△BCD中,
在△ACE和△BCD中,
∵
∴△ACE≌△BCD(SAS).……3分
(2)猜想:△DCE是等腰直角三角形;……4分
理由说明:
∵△A![]() CE≌△BCD,
CE≌△BCD,
∴CE=CD,∠3=∠4.
∵∠4+∠5=90°,
∴∠3+∠5=90°.
即∠E![]() CD=90°.
CD=90°.
∴△DCE是等腰直角三角形.……7分

练习册系列答案
相关题目
 22、已知:如图,Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,试以图中标有字母的点为端点,连接两条线段,如果你所连接的两条线段满足相等,垂直或平行关系中的一种,那么请你把它写出来并证明.
22、已知:如图,Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,试以图中标有字母的点为端点,连接两条线段,如果你所连接的两条线段满足相等,垂直或平行关系中的一种,那么请你把它写出来并证明. 20、已知:如图,Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,且不与A、B两点重合,AE⊥AB,AE=BD,连接DE、DC.
20、已知:如图,Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,且不与A、B两点重合,AE⊥AB,AE=BD,连接DE、DC.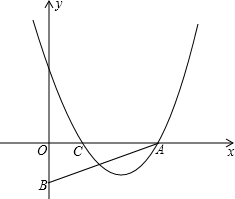 C=OB,抛物线y=(x-2)(x-m)-(p-2)(p-m)(m、p为常数且m+2≥2p>0)经过A、C两点.
C=OB,抛物线y=(x-2)(x-m)-(p-2)(p-m)(m、p为常数且m+2≥2p>0)经过A、C两点.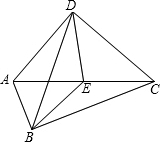 已知:如图,Rt△ABC和Rt△ADC,∠ABC=∠ADC=90°,点E是AC的中点.
已知:如图,Rt△ABC和Rt△ADC,∠ABC=∠ADC=90°,点E是AC的中点.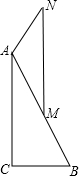 已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AM=AN,MN∥AC.
已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AM=AN,MN∥AC.