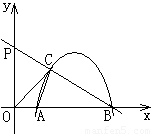
题目内容
开口向下的抛物线![]() 与
与![]() 轴的交点为A、B(A在B的左边),与
轴的交点为A、B(A在B的左边),与![]() 轴交于点C。连结AC、BC。
轴交于点C。连结AC、BC。
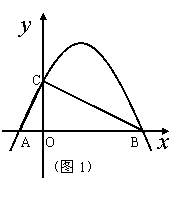
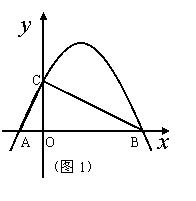
(1) 若△ABC是直角三角形(图1)。求二次函数的解析式;
(2) 在(1)的条件下,将抛物线沿![]() 轴的负半轴向下平移
轴的负半轴向下平移![]() (
(![]() >0)个单位,使平移后的抛物线与坐标轴只有两个交点。求
>0)个单位,使平移后的抛物线与坐标轴只有两个交点。求![]() 的值。
的值。
(3) 当点C坐标为(0,4)时(图2),P、Q两点同时从C点出发,点P沿折线C→O→B运动到点B,点Q沿抛物线(在第一象限的部分)运动到点B,若P、Q两点的运动速度相同,请问谁先到达点B?请说明理由.(参考数据:![]()
![]() )
)

抛物线![]() 与
与![]() 轴的交点为A(-1,0)、B(4,0)
轴的交点为A(-1,0)、B(4,0)
(1) 若△ABC是直角三角形,只有∠ACB=900 。
由题易得△ACO∽△COB
 ∴
∴![]() ∴
∴![]() ∴
∴![]()
∵抛物线开口向下 ∴C(0,2) ………………2分
把 C(0,2)代入得 ![]()
![]()
![]() ………………2分
………………2分
(2)由 ![]() 可得
可得
抛物线的顶点为(![]() ,
,![]() ), 点C(0,2) ………………1分
), 点C(0,2) ………………1分
当点C向下平移到原点时,
平移后的抛物线与坐标轴只有两个交点 ∴![]() ………………1分
………………1分
当顶点向下平移到![]() 轴时,
轴时,
平移后的抛物线与坐标轴只有两个交点 ∴![]() ………………1分
………………1分
(3)当点C为(0,4)时,抛物线的解析式为![]()
抛物线的顶点为D(![]() ,
,![]() ) ………………1分
) ………………1分
连结DC、DB
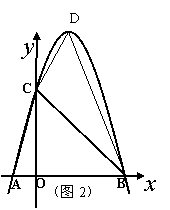 ∵D(
∵D(![]() ,
,![]() ) B(4,0) C(0,4)
) B(4,0) C(0,4)
∴CD=![]()
DB=![]()
∴CD+DB=2.7+6.75=9.45 ………………2分
∵CO+OB=4+4=8 ∴DB+DC>CO+OB
由函数图像可知第一象限内的抛物线的长度比CD+DB还要长
所以第一象限内的抛物线的长度要大于折线C→O→B的长度
所以点P先到达点B ………………2分

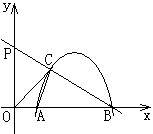
 与
与 轴交于
轴交于 、
、 两点,
两点, 在第一象限,且使
在第一象限,且使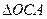 ∽
∽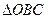 ,(1)求
,(1)求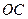 的长及
的长及 的值;(2)
的值;(2) 与
与 轴交于
轴交于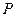 点,点
点,点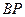 的中点时,求直线
的中点时,求直线
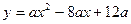 与
与 轴交于
轴交于 、
、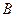 两点,
两点,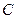 在第一象限,且使
在第一象限,且使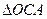 ∽
∽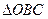 ,(1)求
,(1)求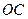 的长及
的长及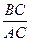 的值;(2)
的值;(2)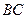 与
与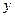 轴交于
轴交于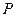 点,点
点,点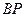 的中点时,求直线
的中点时,求直线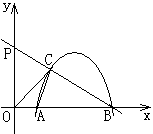
 与
与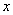 轴交于
轴交于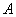 、
、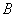 两点,
两点, 在第一象限,且使
在第一象限,且使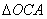 ∽
∽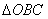 ,(1)求
,(1)求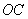 的长及
的长及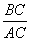 的值;(2)
的值;(2)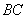 与
与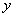 轴交于
轴交于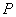 点,点
点,点 的中点时,求直线
的中点时,求直线