题目内容
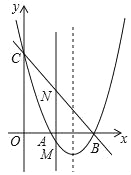
【题目】如图，在
中，
，
于
，将
沿
折叠为
，将
沿
折叠为
，延长
和
相交于点
．
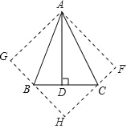
（1）求证：四边形
为正方形；
（2）若
，
，求的长．
【答案】（1）见解析；（2）
【解析】
（1）由折叠的性质可得到的条件是：①AG=AD=AF，②∠GAF=∠GAD+∠DAF=2∠BAC=90°，且∠G=∠F=90°；由②可判定四边形AGHF是矩形，由AG=AF可证得四边形AGHF是正方形；
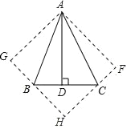
（2）设AD=x，由折叠的性质可得：AD=AF=x（即正方形的边长为x），BG=BD=6，CF=CD=4；进而可用x表示出BH、HC的长，即可在Rt△BHC中，由勾股定理求得AD的长，进而可求出AB的长．
解：（1）
，
；
由折叠可知，
，
，
，
，
；
；
四边形
是正方形，
（2）
四边形是正方形，
，
又
，
，
；
设
的长为
，则
，
．
在
中，
，
，
解得
，
（不合题意，舍去），
，
．
练习册系列答案
相关题目
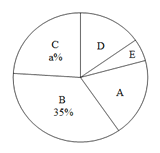
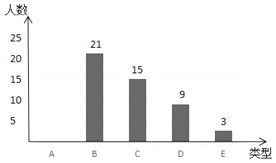
【题目】随着移动终端设备的升级换代，手机己经成为我们生活中不可缺少的一部分，为了解中学生在假期使用手机的情况（选项：A．和同学亲友聊天：B．学习：C．购物：D．游戏：E．其他），端午节后某中学在全校范围内随机抽取了若干名学生进行调查，得到如下图表（部分信息未给出）：
选项 | 频数 | 百分比 |
A | 10 | m |
B | n | 20% |
C | 5 | 10% |
D | p | 40% |
E | 5 | 10% |
合计 | 100% |
根据以上信息解答下列问题：
（1）m＝ ，n＝ ，p＝ ；
（2）补全条形统计图；
（3）若该中学约有800名学生，估计全校学生中利用手机购物或玩游戏的共有多少人？
