题目内容
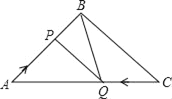
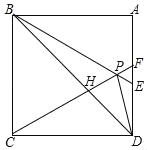
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是_____(填序号)
【答案】①②④
【解析】
由正方形的性质和相似三角形的判定与性质,即可得出结论.
∵△BPC是等边三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°,
∴BE=2AE;故①正确;
∵PC=CD,∠PCD=30°,
∴∠PDC=75°,
∴∠FDP=15°,
∵∠DBA=45°,
∴∠PBD=15°,
∴∠FDP=∠PBD,
∵∠DFP=∠BPC=60°,
∴△DFP∽△BPH;故②正确;
∵∠FDP=∠PBD=15°,∠ADB=45°,
∴∠PDB=30°,而∠DFP=60°,
∴∠PFD≠∠PDB,
∴△PFD与△PDB不会相似;故③错误;
∵∠PDH=∠PCD=30°,∠DPH=∠DPC,
∴△DPH∽△CPD,
∴![]() ,
,
∴DP2=PHPC,故④正确;
故答案是:①②④.

练习册系列答案
相关题目