题目内容
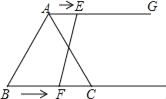
【题目】如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向A点运动,设运动时间为x秒.
(1)x为何值时,PQ∥BC;
(2)是否存在某一时刻,使△APQ∽△CQB?若存在,求出此时AP的长;若不存在,请说明理由;
(3)当![]() =
=![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() cm;(3)
cm;(3)![]() .
.
【解析】
试题本题主要考查了相似三角形的判定与性质、等腰三角形的性质、解方程、两个三角形的面积比等于两个底的比(这两底上的高相等)等知识,利用相似三角形的性质是解决本题的关键.
(1)当PQ∥BC时,根据平行线分线段成比例定理,可得出关于AP,PQ,AB,AC的比例关系式,我们可根据P,Q的速度,用时间x表示出AP,AQ,然后根据得出的关系式求出x的值.
(2)由△APQ∽△CQB得出![]() =
=![]() ,进一步代入求x的值;
,进一步代入求x的值;
(3)当![]() 时得出CQ:AC=1:3,那么CQ=10cm,此时时间x正好是(1)的结果,那么此时PQ∥BC,由此可根据平行这个特殊条件,得出三角形APQ和ABC的面积比,然后再根据三角形PBQ的面积=三角形ABC的面积-三角形APQ的面积-三角形BQC的面积来得出答案即可
时得出CQ:AC=1:3,那么CQ=10cm,此时时间x正好是(1)的结果,那么此时PQ∥BC,由此可根据平行这个特殊条件,得出三角形APQ和ABC的面积比,然后再根据三角形PBQ的面积=三角形ABC的面积-三角形APQ的面积-三角形BQC的面积来得出答案即可
试题解析:解:(1)由题意知AP=4x,CQ=3x,
若PQ∥BC,则△APQ∽△ABC,
![]() =
=![]() ,
,
∵AB=BC=20,AC=30,
∴AQ=30-3x,
∴![]() =
=![]() ,
,
∴x=![]() ,
,
∴当x=![]() 时,PQ∥BC.
时,PQ∥BC.
(2)∵△APQ∽△CQB,则![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴9x-10x=0,
∴x1=0(舍去).x2=![]() .
.
∴当AP的长为![]() cm,△APQ∽△CQB;
cm,△APQ∽△CQB;
(3)∵![]() ,
,
∴![]() =
=![]() ,
,
又∵AC=30,
∴CQ=10,
即3x÷10x=![]() ,
,
此时,AP=4x=![]() ,
,
∴![]() =
=![]() =
=![]() .
.
∴![]() =
=![]() =
=![]() .
.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | | 8 | 0.4 |
乙 | | 9 | | 3.2 |
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).
【题目】新课程改革十分关注学生的社会实践活动,小明在一次社会实践活动中负责了解他所居住的小区500户居民的家庭月人均收入情况,他从中随机调查了40户居民家庭的“家庭月人均收入情况”(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).
分组 | 频数 | 占比 |
1000≤x<2000 | 3 | 7.5% |
2000≤x<3000 | 5 | 12.5% |
3000≤x<4000 | a | 30% |
4000≤x<5000 | 8 | 20% |
5000≤x<6000 | b | c |
6000≤x<7000 | 4 | 10% |
合计 | 40 | 100% |
(1)频数分布表中,a= ,b= ,C= ,请根据题中已有信息补全频数分布直方图;
(2)观察已绘制的频数分布直方图,可以看出组距是 ,这个组距选择得 (填“好”或“不好”),并请说明理由.
(3)如果家庭人均月收入“大于3000元不足6000元”的为中等收入家庭,则用样本估计总体中的中等收入家庭大约有 户.