题目内容
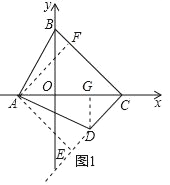
【题目】如图1，在平面直角坐标系中，A（﹣3，0）、B（0，7）、C（7，0），∠ABC+∠ADC＝180°，BC⊥CD．
（1）求证：∠ABO＝∠CAD；
（2）求四边形ABCD的面积；
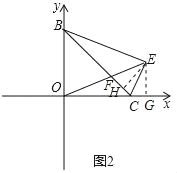
（3）如图2，E为∠BCO的邻补角的平分线上的一点，且∠BEO＝45°，OE交BC于点F，求BF的长．
【答案】（1）见解析；（2）50；（3）7.
【解析】
（1）根据四边形的内角和定理、直角三角形的性质证明；
（2）过点A作AF⊥BC于点F，作AE⊥CD的延长线于点E，作DG⊥x轴于点G，证明△ABF≌△ADE、△ABO≌△DAG，得到D点的坐标为（4，﹣3），根据三角形的面积公式计算；
（3）作EH⊥BC于点H，作EG⊥x轴于点G，根据角平分线的性质得到EH＝EG，证明△EBH≌△EOG，得到EB＝EO，根据等腰三角形的判定定理解答．
（1）在四边形ABCD中，
∵∠ABC+∠ADC＝180°，
∴∠BAD+∠BCD＝180°，
∵BC⊥CD，
∴∠BCD＝90°，
∴∠BAD＝90°，
∴∠BAC+∠CAD＝90°，
∵∠BAC+∠ABO＝90°，
∴∠ABO＝∠CAD；
（2）过点A作AF⊥BC于点F，作AE⊥CD的延长线于点E，作DG⊥x轴于点G，如图1
∵B（0，7），C（7，0），
∴OB＝OC，
∴∠BCO＝45°，
∵BC⊥CD，
∴∠BCO＝∠DCO＝45°，
∵AF⊥BC，AE⊥CD，
∴AF＝AE，∠FAE＝90°，
∴∠BAF＝∠DAE，
在△ABF和△ADE中，
，
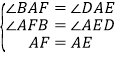∴△ABF≌△ADE（AAS），
∴AB＝AD，
同理，△ABO≌△DAG，
∴DG＝AO，BO＝AG，
∵A（﹣3，0）B（0，7），
∴D（4，﹣3），
S四ABCD＝
AC（BO+DG ）＝50；
（3）过点E作EH⊥BC于点H，作EG⊥x轴于点G，如图2
∵E点在∠BCO的邻补角的平分线上，
∴EH＝EG，
∵∠BCO＝∠BEO＝45°，
∴∠EBC＝∠EOC，
在△EBH和△EOG中，
，
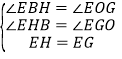∴△EBH≌△EOG（AAS），
∴EB＝EO，
∵∠BEO＝45°，
∴∠EBO＝∠EOB＝67.5°，又∠OBC＝45°，
∴∠BOE＝∠BFO＝67.5°，
∴BF＝BO＝7．
