题目内容
(2012•从化市一模)如图(1),在平面直角坐标系中,抛物线y=ax2+bx-3a经过A(-1,0)、B(0,3)两点,与x轴交于另一点C,顶点为D.
(1)求该抛物线的解析式及点C、D的坐标;
(2)经过点B、D两点的直线与x轴交于点E,若点F是抛物线上一点,以A、B、E、F为顶点的四边形是平行四边形,求点F的坐标;
(3)如图(2)P(2,3)是抛物线上的点,Q是直线AP上方的抛物线上一动点,求△APQ的最大面积和此时Q点的坐标.
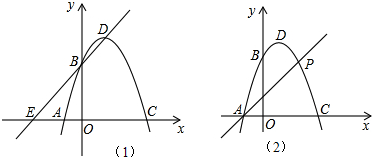
(1)求该抛物线的解析式及点C、D的坐标;
(2)经过点B、D两点的直线与x轴交于点E,若点F是抛物线上一点,以A、B、E、F为顶点的四边形是平行四边形,求点F的坐标;
(3)如图(2)P(2,3)是抛物线上的点,Q是直线AP上方的抛物线上一动点,求△APQ的最大面积和此时Q点的坐标.

分析:(1)首先将点A、B的坐标代入抛物线的解析式中,即可求出待定系数的值.再通过配方、令函数值为0可求出顶点D以及点C的坐标.
(2)由图可知:若以A、B、E、F为顶点的四边形是平行四边形,令EF∥AB显然不符合要求,那么只需考虑BF∥AE即可,那么还需满足BF=AE;首先求出直线BD的解析式,进而得出点E的坐标以及AE、BF的长,由此可确定点F的坐标,再代入抛物线的解析式中验证即可.
(3)分别过点P、Q作x轴的垂线,那么△APQ的面积可由五边形和△APS(以解答图为准)的面积差求得,在得到关于△APQ的面积和Q点横坐标的函数关系式,根据函数的性质即可确定该题的答案.
(2)由图可知:若以A、B、E、F为顶点的四边形是平行四边形,令EF∥AB显然不符合要求,那么只需考虑BF∥AE即可,那么还需满足BF=AE;首先求出直线BD的解析式,进而得出点E的坐标以及AE、BF的长,由此可确定点F的坐标,再代入抛物线的解析式中验证即可.
(3)分别过点P、Q作x轴的垂线,那么△APQ的面积可由五边形和△APS(以解答图为准)的面积差求得,在得到关于△APQ的面积和Q点横坐标的函数关系式,根据函数的性质即可确定该题的答案.
解答:解:(1)∵抛物线y=ax2+bx-3a经过A(-1,0)、B(0,3)两点,有:
,
解得
抛物线的解析式为:y=-x2+2x+3
∵由-x2+2x+3=0,
解得:x1=-1,x2=3
∴C(3,0)
∵由y=-x2+2x+3=-(x-1)2+4
∴D(1,4).
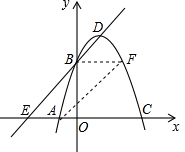 (2)∵四边形AEBF是平行四边形,
(2)∵四边形AEBF是平行四边形,
∴BF=AE.
设直线BD的解析式为:y=kx+b,则
∵B(0,3),D(1,4)
∴
,
解得
∴直线BD的解析式为:y=x+3;
当y=0时,x=-3
∴E(-3,0),∴OE=3,
∵A(-1,0)
∴OA=1,∴AE=2,
∴BF=2,
∴F的横坐标为2,
∴y=3,
∴F(2,3).
(3)如图,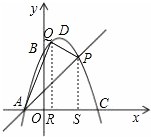 设Q(a,-a2+2a+3),作PS⊥x轴,QR⊥x轴于点S、R,且P(2,3),
设Q(a,-a2+2a+3),作PS⊥x轴,QR⊥x轴于点S、R,且P(2,3),
∴AR=a+1,QR=-a2+2a+3,PS=3,RS=2-a,AS=3
∴S△PQA=S四边形PSRQ+S△QRA-S△PSA
=
×RS+
-
=
×(2-a)+
-
∴S△PQA=-
a2+
a+3=-
(a-
)2+
∴当a=
时,S△PQA的最大面积为
,
此时Q(
,
).
|
解得
|
抛物线的解析式为:y=-x2+2x+3
∵由-x2+2x+3=0,
解得:x1=-1,x2=3
∴C(3,0)
∵由y=-x2+2x+3=-(x-1)2+4
∴D(1,4).
 (2)∵四边形AEBF是平行四边形,
(2)∵四边形AEBF是平行四边形,∴BF=AE.
设直线BD的解析式为:y=kx+b,则
∵B(0,3),D(1,4)
∴
|
解得
|
∴直线BD的解析式为:y=x+3;
当y=0时,x=-3
∴E(-3,0),∴OE=3,
∵A(-1,0)
∴OA=1,∴AE=2,
∴BF=2,
∴F的横坐标为2,
∴y=3,
∴F(2,3).
(3)如图,
 设Q(a,-a2+2a+3),作PS⊥x轴,QR⊥x轴于点S、R,且P(2,3),
设Q(a,-a2+2a+3),作PS⊥x轴,QR⊥x轴于点S、R,且P(2,3),∴AR=a+1,QR=-a2+2a+3,PS=3,RS=2-a,AS=3
∴S△PQA=S四边形PSRQ+S△QRA-S△PSA
=
| (PS+QR) |
| 2 |
| AR×QR |
| 2 |
| PS×AS |
| 2 |
=
| (3-a2+2a+3) |
| 2 |
| (a+1)×(-a2+2a+3) |
| 2 |
| 3×3 |
| 2 |
∴S△PQA=-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 27 |
| 8 |
∴当a=
| 1 |
| 2 |
| 27 |
| 8 |
此时Q(
| 1 |
| 2 |
| 15 |
| 4 |
点评:本题主要考查了二次函数、顶点坐标、平行四边形的性质、三角形的面积等基础知识,考查了计算能力.在解题时,要注意数形结合数学思想的合理应用.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目