题目内容
已知a2-6a+9与|b-1|互为相反数，求代数式(| 4 |
| a2-b2 |
| a+b |
| ab2-a2b |
| a2+ab-2b2 |
| a2b+2ab2 |
| b |
| a |
分析：因为a2-6a+9与|b-1|互为相反数，所以可得（a-3）2+|b-1|=0所以a=3，b=1，通过观察所求的代数式很复杂，化简的过程很繁琐，而a，b的值简单，所以本题比较简便的方法是直接把a，b的值代入求解即可．
解答：解：由已知可得a2-6a+9+|b-1|=0，
即（a-3）2+|b-1|=0，
∴a=3，b=1，
∴原式=（
+
）÷
+
=-
×
+
=
．
即（a-3）2+|b-1|=0，
∴a=3，b=1，
∴原式=（
| 4 |
| 9-1 |
| 3+1 |
| 3-9 |
| 9+3-2 |
| 9+6 |
| 1 |
| 3 |
=-
| 1 |
| 6 |
| 3 |
| 2 |
| 1 |
| 3 |
=
| 1 |
| 12 |
点评：本题所考查的内容“分式的运算”是数与式的核心内容，全面考查了有理数、整式、分式运算等多个知识点，要合理寻求简单运算途径的能力及分式运算．另外还要熟悉相反数的定义，利用定义列出方程求出a，b的值．
练习册系列答案
阅读快车系列答案
相关题目
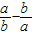）÷（a+b）的值为 ．
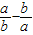）÷（a+b）的值为 ．