题目内容
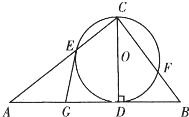 如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA,CB于点E,F,点G是AD的中点.求证:GE是⊙O的切线.
如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA,CB于点E,F,点G是AD的中点.求证:GE是⊙O的切线.
分析:要证GE是⊙O的切线,只要证明∠OEG=90°即可.
解答: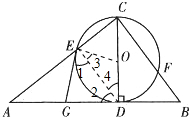 证明:(证法一)连接OE,DE,
证明:(证法一)连接OE,DE,
∵CD是⊙O的直径,
∴∠AED=∠CED=90°,
∵G是AD的中点,
∴EG=
AD=DG,
∴∠1=∠2;
∵OE=OD,
∴∠3=∠4,
∴∠1+∠3=∠2+∠4,
∴∠OEG=∠ODG=90°,
故GE是⊙O的切线;
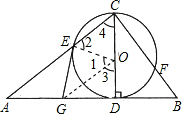 (证法二)连接OE,OG,
(证法二)连接OE,OG,
∵AG=GD,CO=OD,
∴OG∥AC,
∴∠1=∠2,∠3=∠4.
∵OC=OE,
∴∠2=∠4,
∴∠1=∠3.
又OE=OD,OG=OG,
∴△OEG≌△ODG,
∴∠OEG=∠ODG=90°,
∴GE是⊙O的切线.
 证明:(证法一)连接OE,DE,
证明:(证法一)连接OE,DE,∵CD是⊙O的直径,
∴∠AED=∠CED=90°,
∵G是AD的中点,
∴EG=
| 1 |
| 2 |
∴∠1=∠2;
∵OE=OD,
∴∠3=∠4,
∴∠1+∠3=∠2+∠4,
∴∠OEG=∠ODG=90°,
故GE是⊙O的切线;
 (证法二)连接OE,OG,
(证法二)连接OE,OG,∵AG=GD,CO=OD,
∴OG∥AC,
∴∠1=∠2,∠3=∠4.
∵OC=OE,
∴∠2=∠4,
∴∠1=∠3.
又OE=OD,OG=OG,
∴△OEG≌△ODG,
∴∠OEG=∠ODG=90°,
∴GE是⊙O的切线.
点评:本题考查切线的判定方法及圆周角定理运用.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
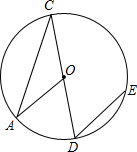 如图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( )
如图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( )| A、25° | B、30° | C、40° | D、50° |
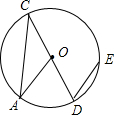 如图,已知CD是⊙O的直径,弦DE∥半径OA,∠D=50°,∠C=( )
如图,已知CD是⊙O的直径,弦DE∥半径OA,∠D=50°,∠C=( )| A、50° | B、40° | C、25° | D、20° |
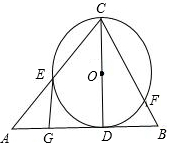 如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O交CA于点E,点G是AD的中点.
如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O交CA于点E,点G是AD的中点.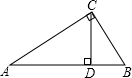 如图,已知CD是Rt△ABC的斜边上的高,其中AD=9cm,BD=4cm,那么CD等于
如图,已知CD是Rt△ABC的斜边上的高,其中AD=9cm,BD=4cm,那么CD等于 (2012•苍梧县二模)如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE,CD相交于点B.
(2012•苍梧县二模)如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE,CD相交于点B.