题目内容
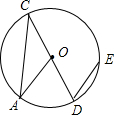如图，已知CD是⊙O的直径，弦DE∥半径OA，∠D=50°，∠C=（ ）| A、50° | B、40° | C、25° | D、20° |
分析：首先根据平行线的性质得到∠D的内错角的度数，再根据等腰三角形的两个底角相等以及三角形的外角的性质求解．
解答：解：∵DE∥OA，∴∠D=∠AOD=50°．
∵OA=OC，∴∠C=∠A=
×50°=25°．
故选C．
∵OA=OC，∴∠C=∠A=
| 1 |
| 2 |
故选C．
点评：解答此题的关键是利用两直线平行的性质、等腰三角形的性质、三角形的外角的性质解答．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
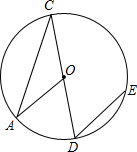如图，已知CD是⊙O的直径，过点D的弦DE平行于半径OA，若∠D的度数是50°，则∠C的度数是（ ）| A、25° | B、30° | C、40° | D、50° |
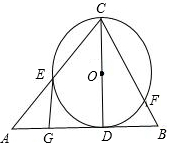如图，已知CD是△ABC中AB边上的高，以CD为直径的⊙O交CA于点E，点G是AD的中点．
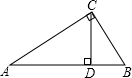如图，已知CD是Rt△ABC的斜边上的高，其中AD=9cm，BD=4cm，那么CD等于
（2012•苍梧县二模）如图，已知CD是⊙O的直径，AC⊥CD，垂足为C，弦DE∥OA，直线AE，CD相交于点B．