题目内容
在平面直角坐标系中,已知线段AB的两个端点分别是A(- 4 ,-1).B(1,1) 将线段AB平移后得到线段A ’B’,若点A的坐标为 (-2 , 2 ) ,则点 B’的坐标为
A . ( 3 , 4 ) B . ( 4 , 3 ) C . (一l ,一2 ) D ,(-2,-1)
A . ( 3 , 4 ) B . ( 4 , 3 ) C . (一l ,一2 ) D ,(-2,-1)
A
各对应点之间的关系是横坐标加1,纵坐标加4,那么让点B的横坐标加1,纵坐标加4即为点B′的坐标.
解:由A(-3,-2)的对应点A′的坐标为(-2,2 ),
坐标的变化规律可知:各对应点之间的关系是横坐标加1,纵坐标加4,
∴点B′的横坐标为1+1=2;纵坐标为2+4=6;
即所求点B′的坐标为(2,6).
故选:A.
解:由A(-3,-2)的对应点A′的坐标为(-2,2 ),
坐标的变化规律可知:各对应点之间的关系是横坐标加1,纵坐标加4,
∴点B′的横坐标为1+1=2;纵坐标为2+4=6;
即所求点B′的坐标为(2,6).
故选:A.

练习册系列答案
相关题目
 上
上
 上
上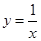
 (
( 为实数)
为实数) 时,
时, 随着
随着 的增大而增大,试求出
的增大而增大,试求出 的一个值
的一个值 (米)与火车行驶时间
(米)与火车行驶时间 (秒)之间的关系用图象描述如图所示,有下列结论:
(秒)之间的关系用图象描述如图所示,有下列结论:
 自变量x取值范围是
自变量x取值范围是 