题目内容
如图，AB为半圆O的直径，C为AO的中点，CD⊥AB交半圆于点D，以C为圆心，CD为半径画弧交AB于E点，若AB=8，则图中阴影部分的面积是（ ）分析：根据图形可得，阴影部分的面积=S半圆-（SADC+S扇形CDE）=S半圆-（S扇形OAD-S△CDO+S扇形CDE），依次运算即可得出答案．
解答：解：连接AD，OD，BD，
可得△ACD∽△CDB，有CD2=AC•CB，
∴CD=2
，OC=2，tan∠COD=2
：2=
：1，
∴S扇形OAD=
=
π，S△CDO=
CO×CD=2
，
∴SADC=S扇形OAD-S△CDO═
π-2
，S扇形CDE=
×π×（2
）2=3π，
∴阴影部分的面积=S半圆-（SADC+S扇形CDE）=
π+2
．
故选A．
可得△ACD∽△CDB，有CD2=AC•CB，
∴CD=2
| 3 |
| 3 |
| 3 |
∴S扇形OAD=
| 60π×42 |
| 360 |
| 8 |
| 3 |
| 1 |
| 2 |
| 3 |
∴SADC=S扇形OAD-S△CDO═
| 8 |
| 3 |
| 3 |
| 1 |
| 4 |
| 3 |
∴阴影部分的面积=S半圆-（SADC+S扇形CDE）=
| 7 |
| 3 |
| 3 |
故选A．
点评：本题考查了扇形的面积计算，涉及了相似三角形的性质，等边三角形的性质，三角形的面积公式，圆的面积公式，综合性较强，注意仔细观察所给图形．
练习册系列答案
阶梯计算系列答案
相关题目
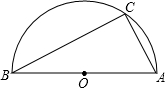
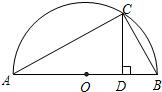为D，AD=a，DB=b．
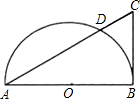如图，AB为半圆O的直径，CB切半圆于点B，AC交半圆于点D，若CD=1，AD=3，则⊙O半径的长为
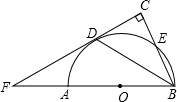C，直线CD交BA的延长线于点F．
如图，AB为半圆O的直径，B1，B2，…，Bk是半圆上的k个点，满足BB1=B1B2=…Bk-1Bk，对于线段OB1，OB2，…，OBk，AB1，AB2，…，ABk，当k=4时，有