题目内容
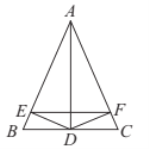
【题目】如图，在△ABC中，AB=AC，AD平分∠BAC，DE⊥AB，DF⊥AC，E、F分别为垂足，则下列四个结论：①∠DEF=∠DFE； ②AE=AF； ③AD平分∠EDF； ④AD垂直平分EF.其中正确结论有（）
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
根据角平分线的性质和等腰三角形的形状可得①④正确；根据全等三角形对应边相等可得AE=AF，∠ADE=∠ADF可得②③正确；
∵AB=AC，∴△ABC是等腰三角形，∠B=∠C．
∵AD平分∠BAC，∴BD=CD．
∵DE⊥AB于E，DF⊥AC于F，∴DE=DF，∴∠DEF=∠DFE，故①正确；
在Rt△ADE和Rt△ADF中，∵
，∴Rt△ADE≌Rt△ADF（HL），∴AE=AF，∠ADE=∠ADF，故②③正确；
∵AE=AF，AD平分∠BAC，∴AD垂直平分EF，故④正确．
故选D．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
