题目内容
(1)解方程: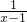 +
+ =1;
=1;
(2)解不等式组: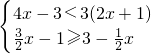 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.

解:(1)方程两边都乘以x(x-1)得:x+2(x-1)=x(x-1),
解这个方程得:x2-4x+2=0,
x=2± ,
,
经检验x=2± 都是原方程的解,
都是原方程的解,
∴原方程的解是x1=2+ ,x2=2-
,x2=2- .
.
(2)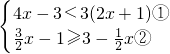 ,
,
解不等式①得:x>-3,
解不等式②得:x≥2,
∴不等式组的解集是x≥2,
在数轴上表示不等式组的解集为: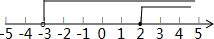 .
.
分析:(1)方程两边都乘以x(x-1),把分式方程转化成整式方程,求出整式方程的解,再代入x(x-1)进行检验即可;
(2)求出不等式①②的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
点评:本题考查了解方程和解一元一次不等式(组)等知识点的应用,解(1)小题的关键是把分式方程转化成整式方程,解(2)小题的关键是根据不等式的解集找出不等式组的解集.解分式方程一定要进行检验呀.
解这个方程得:x2-4x+2=0,
x=2±
 ,
,经检验x=2±
 都是原方程的解,
都是原方程的解,∴原方程的解是x1=2+
 ,x2=2-
,x2=2- .
.(2)
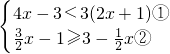 ,
,解不等式①得:x>-3,
解不等式②得:x≥2,
∴不等式组的解集是x≥2,
在数轴上表示不等式组的解集为:
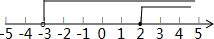 .
.分析:(1)方程两边都乘以x(x-1),把分式方程转化成整式方程,求出整式方程的解,再代入x(x-1)进行检验即可;
(2)求出不等式①②的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
点评:本题考查了解方程和解一元一次不等式(组)等知识点的应用,解(1)小题的关键是把分式方程转化成整式方程,解(2)小题的关键是根据不等式的解集找出不等式组的解集.解分式方程一定要进行检验呀.

练习册系列答案
相关题目