题目内容
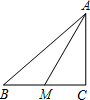
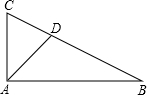
如图,在Rt△ABC中,∠CAB=90°,AD是∠CAB的平分线,tanB=
,则CD:DB=______.
| 1 |
| 2 |

如图,延长BA到E,使AE=AC,连接CE,
则∠E=∠ECA=45°.
∵∠CAD=∠BAD=45°,
∴∠E=∠BAD=45°,
∴CE∥AD.
∴CD:BD=AE:AB,
∵AC=AE,
∴CD:BD=AC:AB,
∵AC:AB=tanB=
,
∴CD:DB=1:2.
故答案为:1:2.

则∠E=∠ECA=45°.
∵∠CAD=∠BAD=45°,
∴∠E=∠BAD=45°,
∴CE∥AD.
∴CD:BD=AE:AB,
∵AC=AE,
∴CD:BD=AC:AB,
∵AC:AB=tanB=
| 1 |
| 2 |
∴CD:DB=1:2.
故答案为:1:2.


练习册系列答案
相关题目