题目内容
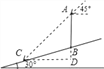
【题目】如图,在一个坡角为30°的斜坡上有一电线杆AB,当太阳光与水平线成45°角时,测得该杆在斜坡上的影长BC为20m.求电线杆AB的高(精确到0.1m,参考数值:![]() ≈1.73,
≈1.73,![]() ≈1.41).
≈1.41).

【答案】7.3m
【解析】试题分析:过点C作CD⊥AB交AB延长线于点D,先求出CD和BD的长度,再根据直角三角形的性质求出AD的长度,便可求出求电线杆AB的高.
试题解析:解:过点C作CD⊥AB交AB延长线于点D.
在Rt△BCD中,BD=BCsin∠BCD=20×sin30°=10,CD=BCcos30°=20×![]() =
=![]() .
.
在Rt△ACD中,∵∠ACD=45°,∴∠DAC=∠ACD=45°,则AD=CD=![]() ,
,
∴AB=AD﹣BD=![]() ﹣10=10(
﹣10=10(![]() ﹣1)≈10(1.73﹣1)=7.3(m),
﹣1)≈10(1.73﹣1)=7.3(m),
所以,电线杆AB的高约为7.3m.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目