题目内容
【题目】将如图所示的一块直角三角板放置在△ABC上,使三角板的两条直角边DE、EF分别经过点B、C,若∠A=65°,则∠ABE+∠ACE= . 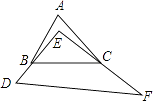
【答案】25°
【解析】解:在△EBC中,∵∠EBC+∠ECB+∠E=180°,
而∠E=90°,
∴∠EBC+∠ECB=90°;
在Rt△ABC中,
∵∠ABC+∠ACB+∠A=180°,
即∠ABE+∠EBC+∠ECB+∠ACE+∠A=180°,
而∠EBC+∠ECB=90°,
∴∠ABE+∠ACE=90°﹣∠A=25°;
所以答案是:25°.
【考点精析】掌握三角形的内角和外角是解答本题的根本,需要知道三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
相关题目