Question

【题目】如图，点E在边长为4的正方形ABCD的边AD上，点A关于BE的对称点为A′，延长EA′交DC于点F，若CF=1cm，则AE=m．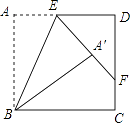

Answer 1

【答案】2.4
【解析】解：连接BF，
设AE=x，
由翻折变换的性质可知，AB=A′B，∠EA′B=∠A=90°，A′E=x，
在Rt△BAE和Rt△BA′E中，
，
∴Rt△BAE≌Rt△BA′E，
∴A′F=FC=1，
又DE=4﹣x，EF=x+1，DF=3，
由勾股定理得，EF2=DE2+DF2 ，
即（x+1）2=（4﹣x）2+9，
解得x=2.4．
所以答案是：2.4．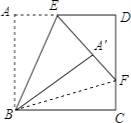

【考点精析】掌握翻折变换（折叠问题）是解答本题的根本，需要知道折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．